Actualizado por ultima vez el 16 de noviembre de 2021, por Luis Benites.
¿Qué es el análisis multivariado?
El análisis multivariante se utiliza para estudiar conjuntos de datos más complejos que los que pueden manejar los métodos de análisis univariante . Este tipo de análisis casi siempre se realiza con software (es decir, SPSS o SAS ), ya que trabajar manualmente con los conjuntos de datos más pequeños puede resultar abrumador.
El análisis multivariante puede reducir la probabilidad de errores de tipo I. A veces, se prefiere el análisis univariado ya que las técnicas multivariadas pueden dificultar la interpretación de los resultados de la prueba. Por ejemplo, las diferencias de grupo en una combinación lineal de variables dependientes en MANOVA pueden no estar claras. Además, el análisis multivariante no suele ser adecuado para pequeños conjuntos de datos.
Hay más de 20 formas diferentes de realizar un análisis multivariado. El que elija depende del tipo de datos que tenga y cuáles sean sus objetivos. Por ejemplo, si tiene un solo conjunto de datos, tiene varias opciones:
- Los árboles aditivos , el escalado multidimensional y el análisis de conglomerados son adecuados cuando las filas y las columnas de la tabla de datos representan las mismas unidades y la medida es una similitud o una distancia.
- El análisis de componentes principales (PCA) descompone una tabla de datos con medidas correlacionadas en un nuevo conjunto de medidas no correlacionadas.
- El análisis de correspondencia es similar al PCA. Sin embargo, se aplica a las tablas de contingencia.
Aunque existen límites bastante claros con un conjunto de datos (por ejemplo, si tiene un único conjunto de datos en una tabla de contingencia, sus opciones se limitan al análisis de correspondencia ), en la mayoría de los casos podrá elegir entre varios métodos.
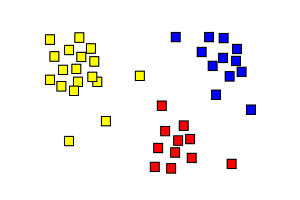
Análisis de conglomerados que muestra tres grupos.
Haga clic en un tema para leer sobre tipos específicos de análisis multivariante:
- Árbol Aditivo.
- Análisis de correlación canónica.
- Análisis de conglomerados.
- Análisis de Correspondencias / Análisis de Correspondencias Múltiples.
- Análisis factorial .
- Análisis generalizado de Procusto .
- Homogeneidad de la covarianza
- Análisis de componentes independientes.
- MANOVA.
- Escalamiento multidimensional.
- Análisis de regresión multiple.
- Regresión de mínimos cuadrados parciales.
- Análisis de Componentes Principales / Regresión / PARAFAC.
- Análisis de redundancia.
Relacionada:
Análisis de componentes independientes
El análisis de componentes independientes se utiliza en estadísticas y procesamiento de señales para expresar una función multivariada por sus factores ocultos o subcomponentes. Estas señales de componentes son señales no gaussianas independientes y la intención es que estas subcomponentes independientes representen con precisión la señal compuesta.
El » problema del cóctel » es un ejemplo citado con frecuencia del análisis de componentes independientes en funcionamiento. Suponga que tiene un cóctel ruidoso, con muchas conversaciones en la misma habitación. Ahora suponga que tiene una serie de micrófonos ubicados en varios lugares de la sala, recogiendo los datos de sonido. Sin conocimiento previo de los altavoces, ¿puede separar la señal de cada micrófono (en cada caso, una combinación de todo el ruido de la sala) en sus componentes, es decir, la voz de cada altavoz?
Puede hacer un trabajo sorprendentemente bueno, suponiendo que tenga suficientes puntos de observación. Si hay N fuentes de ruido ( N invitados, por ejemplo), necesitará N micrófonos para determinar completamente las señales originales.
Supuestos en el Análisis de Componentes Independientes.
El análisis de componentes independientes solo funciona si las fuentes no son gaussianas (es decir, tienen distribuciones no normales ), y esa es una de las primeras suposiciones que hace si usa este análisis en una función multivariante . Dado que está intentando descomponer la función en componentes independientes, también supone que las fuentes originales eran, de hecho, independientes.
Efectos de mezcla en análisis de componentes independientes
Hay tres principios de mezcla de señales que constituyen la base para el análisis de componentes independientes.
- Mezclar señales implica pasar de una serie de señales independientes a una serie de señales dependientes . Aunque todas las señales de origen se generan de forma independiente, las señales compuestas se crean a partir de las mismas señales de origen y, por lo tanto, no pueden ser independientes entre sí.
- Aunque nuestras señales fuente no son gaussianas (según la suposición que hicimos al principio), las señales compuestas son de hecho gaussianas ( normalmente distribuidas ). Esto es por el Teorema del Límite Central , que nos dice que la función de distribución de probabilidad de la suma de variables independientes con varianza finita (como nuestras señales) tenderá hacia la distribución Gaussiana.
- La complejidad de una mezcla de señales siempre debe ser mayor o igual que la complejidad de su señal fuente más simple .
Estos tres principios forman la base del análisis de componentes independientes.
Análisis de componentes independientes: referencias
Hyvarinen, Aapo. ¿Qué es el análisis de componentes independientes? Recuperado de https://www.cs.helsinki.fi/u/ahyvarin/whatisica.shtml el 10 de abril de 2018
Hyvärinen, Karhunen y Oja. (2001). Análisis de componentes independientes . Wiley Interscience.
Ng, Andrés. CS 229 Apuntes de clase: Análisis de componentes independientes. Recuperado de http://cs229.stanford.edu/notes/cs229-notes11.pdf el 10 de abril de 2018
Stone, James. Análisis de componentes independientes. Encyclopedia of Statistics in Behavioral Science, volumen 2, págs. 907–912
Obtenido de https://pdfs.semanticscholar.org/6cdc/d22d69479c6c19f1583a281a95bc4029631e.pdf el 10 de abril de 2018
Otras referencias
Beyer, WH CRC Standard Mathematical Tables, 31ª ed. Boca Raton, FL: CRC Press, págs. 536 y 571, 2002.
Dodge, Y. (2008). La Enciclopedia Concisa de Estadística . Saltador.
Kotz, S.; et al., editores. (2006), Enciclopedia de Ciencias Estadísticas , Wiley.
Vogt, WP (2005). Diccionario de estadística y metodología: una guía no técnica para las ciencias sociales . SABIO.
