Actualizado por ultima vez el 18 de octubre de 2022, por Luis Benites.
Los Números de Bell y el Triángulo de Bell (a veces llamado el triángulo de Pierce o la matriz de Aitken) son una secuencia de números que cuentan las posibles particiones de un conjunto, y el triángulo que facilita su derivación.
Números de Bell: qué son y qué significan
Los primeros números de Bell son:
1, 1, 2, 5, 15, 52, 203, 877, 4140, 21147, 115975.
El n -ésimo número de Bell, Bn , es el número de subconjuntos no vacíos en los que se puede dividir un conjunto de tamaño n. B 0 se define como uno (es decir, el primer número de la lista anterior); Solo hay una partición posible del conjunto que contiene un miembro, por lo que B 1 = 1.
Hay dos particiones posibles para un conjunto con dos elementos, por lo que B 2 es solo dos.
Un conjunto con tres elementos se puede dividir de cinco maneras. Tomando el conjunto {a, b, c}, las cinco particiones posibles son:
- {(a B C)},
- {(a B C)},
- {(a, c) (b)},
- {(b, c), a},
- {(a B C)}.
No existe una fórmula simple que nos pueda dar B n , pero podemos encontrar los números de Bell en el Triángulo de Bell, en la siguiente sección, o usar la siguiente ecuación recursiva para definirlos:
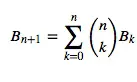
Números de Bell y el Triángulo de Bell como forma de derivarlos
El triángulo de Bell es un triángulo rectángulo fácil de completar que nos da, en la columna de la izquierda, todos los números de Bell.
1. Creando el Triángulo
Haz el triángulo de esta manera:
- En la fila uno, escribe el número 1
- Comience todas las demás filas con el último número de la fila anterior. El último número en la fila 1 fue 1, por lo que la fila 2 también comienza con 1.
- Todos los demás números se encuentran sumando el último número al que está arriba. Para saber qué escribir en el segundo lugar de la fila 2, observamos el lugar anterior, el lugar 1. Esto es solo 1, y el dígito 1 está arriba, por lo que 1 + 1 = 2
Por lo tanto, la primera parte del triángulo de Bell será
1
1 2
Siguiendo esas mismas reglas, comenzamos la tercera fila con el último número de la fila anterior, o 2. Luego sumamos ese 2 al número de arriba para encontrar que el siguiente número es 3. Tres más los dos de arriba hacen cinco, entonces la fila termina con un cinco.
1
1 2
2 3 5
La fila cuatro comienza con el último de la fila tres, es decir, 5. Luego 5 + 2 = 7, por lo que el siguiente lugar es 7 y 7 + 3 = 10, por lo que el siguiente dígito es diez. Terminando esta fila y la siguiente de la misma manera, obtenemos
1
1 2
2 3 5
5 7 10 15
15 20 27 37 52
Para cualquier fila k, el número que comienza la fila es B k-1 . Así que el primer dígito de la fila 1 es B 1 -1 = B(0), el primer dígito de la fila 4 es B(3), y el primer dígito de la fila 55 será B(54).
2. Lectura del Triángulo
Los números de Bell se dan en la columna de la izquierda , en negrita aquí:
1
1 2
2 3 5
5 7 10 15
15 20 27 37 52
Tenga en cuenta que el triángulo a veces se refleja, por lo que los números de Bell aparecen en la columna derecha y no en la izquierda; Asegúrate de conocer la construcción del triángulo antes de intentar leerlo.
Referencias
Guichard, D. Combinatoria y teoría de grafos. Recuperado de
https://www.whitman.edu/mathematics/cgt_online/book/section01.04.html el 4 de febrero de 2018
Weisstein, Eric W. “Bell Triangle”. De MathWorld: un recurso web de Wolfram. http://mathworld.wolfram.com/BellTriangle.html

