Coeficiente de Asociación: Definición, Tipos, Ejemplos

Actualizado el 17 de agosto de 2021, por Luis Benites.

¿Qué es un coeficiente de asociación?

Un coeficiente de asociación mide la fuerza de una relación. “Asociación” significa que las variables tienen elementos compartidos o comunes o algún grado de concordancia.

Está disponible un gran número de diferentes coeficientes de asociación. El que elija depende de muchos factores, incluido el tipo de datos (p. ej ., Tau de Kendall para variables nominales clasificadas o Y de Yule para variables binarias ). Dicho esto, un coeficiente de asociación es independiente de su escala de medida .

Estos coeficientes suelen oscilar entre 0 y 1, donde 0 es sin relación y 1 es una relación perfecta. Sin embargo, algunas medidas de asociación varían de -1 a 1, donde -1 indica una relación inversa perfecta.

Coeficiente de Asociación para Variables Nominales

Tau de Kendall (Coeficiente de correlación de clasificación de Kendall) mide las relaciones entre columnas de datos clasificados.

• Tau-A y Tau-B se suelen utilizar para tablas cuadradas (con columnas y filas iguales).
• Tau-B se ajustará a los rangos empatados.
• Tau-C se suele utilizar para mesas rectangulares. Para mesas cuadradas, Tau-B y Tau-C son esencialmente iguales.

Variables binarias

1. Coeficiente de coligación (Y de Yule)

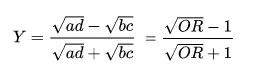
Yules Y (Coeficiente de Coligación) o, más simplemente, Y, puede usarse para aproximar la correlación tetracórica (Warren’s, 2008); La correlación tetracórica se usa para medir el acuerdo del evaluador para datos binarios. La Y de Yule, una transformación de la razón de probabilidades , no se usa con mucha frecuencia. Una de las razones es que su uso generalmente se restringe a tablas de 2×2; Además, el coeficiente H de Digby (1983) generalmente se considera una mejor aproximación.

Los coeficientes Q de Yule, Y de Yule y H de Digby son parte de una familia general de coeficientes que elevan la razón de probabilidades a una potencia (c) (Bonnett & Price, 2007).

• Q de Yule: c = 1
• Y de Yule: c = .5 (es decir, la raíz cuadrada del OR)
• H de Digby = .75

2. Coeficiente de asociación Phi

El coeficiente de asociación Phi se utiliza para tablas de contingencia cuando:

• Al menos una variable es una variable nominal.
• Ambas variables son variables dicotómicas.

La V de Cramer es una medida similar, que se usa cuando las mesas son de 3×3 o más grandes.

Medidas relacionadas

• El coeficiente de contingencia indica si dos variables son dependientes o independientes entre sí.
• Un coeficiente beta estandarizado compara la fuerza de los efectos de las variables independientes sobre las variables dependientes.
• Eta-cuadrado a veces se denomina coeficiente de asociación, aunque se usa para un propósito muy limitado en ANOVA: medir la proporción de varianza entre grupos.
• El coeficiente de correlación de concordancia de Lin mide pares bivariados de observaciones en relación con una prueba o medición de » estándar de oro «.
• El coeficiente de concordancia («estadística W») mide el acuerdo entre diferentes evaluadores.
• El coeficiente de correlación biserial puntual mide la relación entre dos variables: una variable continua ( escala de razón o escala de intervalo ) y una variable naturalmente binaria .

Ver también: Actas de Asociación .

Referencias

Bonett, DG y Price, RM, (2007) Inferencia estadística para coeficientes de Yule generalizados en tablas de contingencia de 2 x 2. Métodos e investigación sociológicos, 35, 429-446.
Digby, PGN (1983). Aproximación del coeficiente de correlación tetracórica. Biometría, 39, 753–757.
Warrens, M. (2008). Sobre coeficientes de asociación para tablas de 2×2 y propiedades que no dependen de las distribuciones marginales. psicometria. 2008 diciembre; 73(4): 777–789. Publicado en línea el 23 de julio de 2008. doi: 10.1007/s11336-008-9070-3.
Yule, GU (1912). Sobre los métodos de medición de la asociación entre dos atributos. Revista de la Sociedad Real de Estadística, 75, 579–652.