Actualizado por ultima vez el 27 de abril de 2022, por Luis Benites.
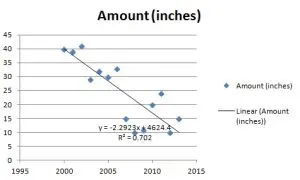
Los coeficientes no estandarizados se utilizan en el análisis de regresión.
Los coeficientes no estandarizados son coeficientes ‘en bruto’ producidos por análisis de regresión cuando el análisis se realiza en variables originales no estandarizadas. A diferencia de los coeficientes estandarizados, que son coeficientes normalizados sin unidades, un coeficiente no estandarizado tiene unidades y una escala de «vida real».
Un coeficiente no estandarizado representa la cantidad de cambio en una variable dependiente Y debido a un cambio de 1 unidad en la variable independiente X.
Uso de coeficientes no estandarizados en regresión
Los coeficientes no estandarizados suelen ser intuitivos de interpretar y comprender. Dado que representan la relación entre datos sin procesar, se pueden usar directamente en cálculos y análisis. También se pueden usar para hacer comparaciones dentro de la ecuación de regresión cuando solo se usa una escala de medición. Si se utilizan varias escalas de medición, se prefieren los coeficientes estandarizados para la comparación (ver más abajo).
Punto débil de un coeficiente no estandarizado
Los coeficientes no estandarizados son menos útiles para la comparación directa cuando las escalas de medición de las variables independientes son diferentes. En estos casos, un número mayor aún puede apuntar a un efecto más pequeño, y para identificar el tamaño del efecto de las variables, es posible que desee estandarizar primero sus coeficientes.
Por ejemplo, en un análisis en el que realiza una regresión de las puntuaciones de CI en los años de universidad y el nivel de ingresos, sus variables estarán en escalas completamente diferentes y, por lo tanto, cada coeficiente no estandarizado (uno en CI/$ y uno en CI/años) no puede ser en comparación con otro coeficiente no estandarizado. Para averiguar cuál es el efecto más interesante, primero se desearía estandarizar los coeficientes , lo que significa que ambos estarían en términos de desviaciones estándar y se compararían fácilmente entre sí.
Referencias
Levine, D. (2014). Incluso usted puede aprender estadísticas y análisis: una guía fácil de entender sobre estadísticas y análisis, 3.ª edición. Pearson FT Press
Janda, Kenneth. Regresión lineal. Lecture Notes from Elementary Statistics for Political Research, 310. Obtenido de http://janda.org/c10/Lectures/topic04/L25-Modeling.htm el 19 de julio de 2018
Wuensch, Tindall, David. Algunas notas sobre la interpretación estadística. Sociología 502 Apuntes de clase. Recuperado de http://faculty.arts.ubc.ca/tindall/soci502/overheads+slides/Statistics_I/Notes_on_Interpretation.pdf el 19 de julio de 2018. Karl. Coeficientes de regresión: no estandarizados versus estandarizados. Recuperado de http://core.ecu.edu/psyc/wuenschk/MV/multReg/Standardized_Regression_Coficients.docx el 19 de julio de 2018.

