Actualizado por ultima vez el 9 de junio de 2022, por Luis Benites.
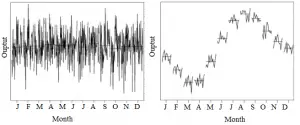
Una serie estacionaria de covarianza (izquierda) y una serie no estacionaria (derecha).
Un proceso estacionario de covarianza (a veces llamado simplemente estacionario ) no cambia a través de los cambios de tiempo. Específicamente, los dos primeros momentos ( media y varianza) no cambian con respecto al tiempo. Estos tipos de procesos proporcionan modelos “apropiados y flexibles” (Pourahmadi, 2001).
El concepto es importante en series de tiempo , donde los coeficientes de correlación entre dos series solo tienen significado si ambas series son estacionarias en covarianza. Cuando una serie no es estacionaria en covarianza, cualquier estimación del modelo no tendrá significado económico (Defusco, 2015).
¿Cómo sé si mi serie es estacionaria en covarianza?
En una serie de tiempo, una variable es estacionaria en covarianza si se cumple lo siguiente (Watsham y Parramore, 1997):
- El valor esperado E(X t ), es una constante finita para todo t,
- la varianza (σ 2 } es una constante finita para todo t,
- El coeficiente de correlación entre X t y X t – n es igual para todo t.
Además, la covarianza de la serie temporal consigo misma debe ser constante y finita para todos los números fijos de periodos pasados o futuros (DeFusco, 2015).
En general, debería poder ver si su serie de tiempo tiene una media y una varianza constantes al graficarla. Además, querrá realizar una prueba de Dickey Fuller aumentada para una raíz unitaria . Una raíz unitaria es una tendencia estocástica en una serie de tiempo, una «caminata aleatoria con deriva» que genera patrones impredecibles. Si su modelo falla la prueba ADF, entonces su proceso no es estacionario en covarianza.
Artículo relacionado: ¿Qué es una secuencia estacionaria? (CalculusHowTo.com).
Referencias
De Fusco, R. et al., (2015). Análisis cuantitativo de inversiones , Wiley.
Pourahmadi, M. (2001). Fundamentos del Análisis de Series Temporales y Teoría de Predicción . Wiley.
Watsham, T. y Parramore, K. (1997). Métodos Cuantitativos en Finanzas. Prensa comercial internacional de Thomson.

