Actualizado por ultima vez el 15 de abril de 2022, por Luis Benites.
Mire el video para obtener una descripción general de la relación de probabilidades y un par de ejemplos de cálculos, o lea a continuación:
Razón de probabilidades Mira este video en YouTube .
¿No puedes ver el vídeo? Haga clic aquí
¿Qué son las «Probabilidades»?
Definiciones de estadísticas >
Definición de probabilidades
Las probabilidades generalmente se definen en estadísticas como la probabilidad de que ocurra un evento dividida por la probabilidad de que no ocurra [1]. En otras palabras, es una proporción de éxitos (o victorias) a pérdidas (o fracasos). Por ejemplo, si un caballo de carreras corre 100 carreras y gana 20 veces, las probabilidades de que el caballo gane una carrera son 20/80 = 1/4.
La definición de cuotas anterior es la cuota a favor de un evento . Pero hay otra forma de definir las probabilidades en las estadísticas: las probabilidades de que ocurra un evento. Esto se define como el número de formas en que un evento no ocurre frente al número de formas en que ocurre un evento [2]. Para nuestro ejemplo del caballo de carreras, eso sería 80 a 20, o 4 a 1.
Cuotas frente a probabilidad
La definición de probabilidades es muy similar a la definición de probabilidad , que es la fracción de veces que ocurre un evento en un cierto número de intentos. En el ejemplo del caballo, la probabilidad de ganar es 20/100.
Cuando hay un número muy pequeño de eventos, las cuotas y la probabilidad son muy similares. Por ejemplo, digamos que el caballo corre 4 carreras y gana 1. La probabilidad de que el caballo gane una carrera es 1/3 (1 victoria contra 3 derrotas) y la probabilidad es 1/4 (1 victoria en 4 carreras).
Una de las principales diferencias entre las cuotas y la probabilidad es que, mientras que las cuotas oscilan entre 0 e infinito, la probabilidad oscila entre 0 y 1.
Definición de diccionario de probabilidades
La definición estadística de probabilidades es bastante precisa en comparación con las definiciones de diccionario, que son inconsistentes y tienen diferentes significados, incluso en un lenguaje sencillo en lugar de uno estadístico [2]:
- “las posibilidades de que algo suceda” (Macmillan British Dictionary, 2012)
- “la probabilidad de que una cosa sea así o suceda en lugar de otra; la relación entre la probabilidad de un evento y la de un evento alternativo” (Diccionario Merriam-Webster, 2012)
- “la relación entre la probabilidad de que ocurra un evento y la probabilidad de que no ocurra; la probabilidad de que ocurra una cosa en lugar de que ocurra otra cosa, como en un concurso” (American Heritage Dictionary, 2012)
¿Qué es la razón de probabilidades?
Una razón de posibilidades (OR) es una medida de asociación entre una determinada propiedad A y una segunda propiedad B en una población . Específicamente, le dice cómo la presencia o ausencia de la propiedad A tiene un efecto sobre la presencia o ausencia de la propiedad B. El OR también se usa para determinar si una exposición en particular (como comer carne procesada) es un factor de riesgo para una determinada resultado (como el cáncer de colon), y comparar los diversos factores de riesgo para ese resultado. Podría usar el OR para averiguar cuánto alcohol conduce a la enfermedad hepática. O tal vez desee averiguar si el uso de teléfonos celulares tiene algún vínculo con el cáncer cerebral. Siempre que tenga dos propiedades que crea que están vinculadas, puede calcular las probabilidades.
Cómo calcular la razón de probabilidades
Tiene dos opciones para la fórmula:
(a/c) / (b/d)
o, de manera equivalente:
(a*d) / (b*c)
Pasos generales:
Paso 1: Calcular las probabilidades de que un miembro de la población tenga la propiedad «A». Suponga que la persona ya tiene «B».
Paso 2: Calcular las probabilidades de que un miembro de la población tenga la propiedad “A”. Suponga que la persona no tiene «B».
Paso 3: Divida el paso 1 por el paso 2 para obtener la razón de probabilidades (OR).
Ejemplo de razón de probabilidades
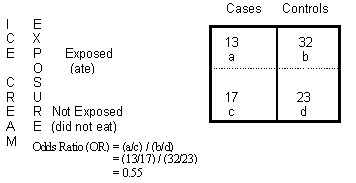
Imagen: Michigan.gov
La imagen de arriba muestra dos niveles de exposición al helado: los que lo comieron y los que no. La tabla 2×2 también muestra dos niveles de resultados: personas que estaban enfermas («casos») y personas que no lo estaban («controles»). La razón de probabilidades se calcula de la siguiente manera:
- Personas enfermas : personas que comieron helado / personas que no = 13/17
- Personas que no están enfermas : personas que comieron helado / personas que no = 32/23
- Dividiendo los dos resultados, obtenemos (13/17) / (32/23) = 0,55
La razón de probabilidad resultante de .55 significa que las personas enfermas tenían aproximadamente la mitad de probabilidades de comer helado que las personas sanas.
Interpretación de la razón de probabilidades; ¿Qué significan los resultados?
- Una razón de probabilidades de exactamente 1 significa que la exposición a la propiedad A no afecta las probabilidades de la propiedad B.
- Una relación de probabilidades de más de 1 significa que hay una mayor probabilidad de que ocurra la propiedad B con la exposición a la propiedad A.
- Una relación de probabilidades menor que 1 se asocia con probabilidades más bajas.
Sin embargo, no es tan simple como eso. Se podría pensar que la relación de probabilidades es demasiado simplista para describir situaciones del mundo real. Si, por ejemplo, tiene un OR positivo, no significa que tenga un resultado estadísticamente significativo. Para averiguarlo, debe considerar el intervalo de confianza y los valores p (si los conoce). El otro problema es que incluso si determina que sus resultados son estadísticamente significativos , es posible que esa importancia no se aplique a todos los miembros de una población; casi siempre hay una multitud de factores asociados con el riesgo. Por ejemplo, este artículo señala que si bien en general, la depresión está fuertemente ligada al suicidio, “…en una muestra particular, con un tamaño y composición particular, y en presencia de otras variables , la asociación puede no ser significativa”.
Población promediada frente a razón de probabilidades específicas del sujeto
Los modelos de población promediada comparan las distribuciones marginales y brindan una descripción general del efecto en una población completa. Los márgenes de una tabla de contingencia contienen los totales, por lo que tiene sentido que se utilicen para calcular la razón de probabilidad marginal para toda la población. Por otro lado, los modelos específicos de materias analizan las distribuciones conjuntas : condiciones o experiencias específicas dentro del modelo. Las distribuciones conjuntas se utilizan para calcular las razones de probabilidades condicionales.
Ejemplo de razón de probabilidades marginales (para modelos de población promediada)
Michael Radelet estudió los datos de sentencias de muerte de Florida de 1976 a 1977.* Calcule la razón de probabilidades marginales para la raza del acusado y si eso marcó o no una diferencia sobre si recibió la pena de muerte:
| Raza demandada | Raza víctima | Pena de muerte Y | Pena de muerte norte |
| W | W | 19 | 132 |
| W | B | 0 | 9 |
| B | W | 11 | 52 |
| B | B | 6 | 97 |
Solución :
- Sumar (marginar) los valores de la tabla. Solo nos interesa la raza del acusado y si recibió o no la pena de muerte. Por lo tanto, podemos marginar (sumar) valores para la raza de la víctima. Esto crea una nueva tabla 2×2:
Raza demandada Muerte Y muerte norte W 19 141 B 17 149 - Use la información en la tabla marginal para encontrar el OR (usando la fórmula OR de arriba):
OR = (a/c) / (b/d) = (19/17)/(141/149) = 1.12/0.95 = 1.18.
Las probabilidades de que un acusado blanco reciba la pena de muerte son 1,18 veces mayores que las de un acusado negro.
*Si está interesado en sus hallazgos, concluyó que no hay pruebas claras que respalden la hipótesis de que la raza del acusado está fuertemente asociada con la imposición de la pena de muerte. Sin embargo, era más probable que los acusados fueran condenados a muerte si tenían una víctima blanca.
Los modelos específicos de sujetos calculan la razón de probabilidades utilizando la misma fórmula que en todos los ejemplos anteriores. La única diferencia es que en lugar de sumar todas las variables, mantendrá constante una variable (es decir, utilizará distribuciones conjuntas).
Siguiente : Razón de probabilidades ajustada
Referencias
[1] La diferencia entre «probabilidad» y «cuotas». Recuperado el 26 de noviembre de 2021 de: https://sphweb.bumc.bu.edu/otlt/mph-modules/bs/bs704_confidence_intervals/BS704_Confidence_Intervals10.html[2] Fulton, L. et al. Confusión entre probabilidades y probabilidades, ¿una pandemia?
Journal of Statistics Education, volumen 20, número 3 (2012) 3
www.amstat.org/publications/jse/v20n3/fulton.pdf
Agresti A. (1990) Análisis de datos categóricos. John Wiley and Sons, Nueva York.
Radelet, ML Características Raciales y la Imposición de la Pena de Muerte. American Sociological Review, v46 n6 p918-27 de diciembre de 1981
Levine, D. (2014). Incluso usted puede aprender estadísticas y análisis: una guía fácil de entender sobre estadísticas y análisis, 3.ª edición. Prensa Pearson FT
