Distribución multivariante: definición

Actualizado el 22 de octubre de 2021, por Luis Benites.

Las distribuciones multivariadas muestran comparaciones entre dos o más medidas y las relaciones entre ellas. Para cada distribución univariante con una variable aleatoria , existe una distribución multivariante más general. Por ejemplo, la distribución normal es univariante y su contraparte más general es la distribución normal multivariante . Si bien el modelo normal multivariado es el modelo más utilizado para analizar datos multivariados [1], hay muchos más: la distribución lognormal multivariada, la distribución binomial multivariada, etc.

Una distribución bivariada es la distribución multivariada más simple, compuesta por un par de variables aleatorias. Sin embargo, al menos teóricamente, podrías tener un número infinito de pares; todos los resultados de una distribución bivariada para dos pares pueden generalizarse a n variables aleatorias.

Probabilidades conjuntas y distribuciones multivariadas

Cada variable aleatoria en una distribución multivariante tiene su propia media y varianza: no hay una función de densidad de probabilidad de «talla única» , como la que encontraría con una distribución univariante. Para variables aleatorias discretas , distribución multivariada y descrita por probabilidades conjuntas. Para variables aleatorias continuas , la distribución univariante relevante se extiende. Sin embargo, una vez que se sumerge en las profundidades de las distribuciones multivariadas, el análisis se vuelve un poco más complicado. Dado que el análisis multivariante implica observaciones vectoriales , la comprensión de la matriz de varianza-covarianza es «vital» para comprender las distribuciones normales multivariantes [2].

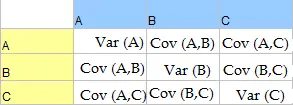
La matriz de varianza-covarianza es clave para comprender una distribución multivariada.

Distribución multinomial vs multivariante

Las distribuciones multinomial y multivariante comparten muchas similitudes, pero hay una diferencia importante: una distribución multinomial tiene una variable dependiente con más de un resultado (es decir, la variable dependiente tiene dos o más niveles ), mientras que una distribución multivariante tiene más de un resultado dependiente. variable.

Referencias