Modelos Semiparamétricos: Definición Simple y Ejemplos

Actualizado el 21 de julio de 2024, por Luis Benites.

Un modelo semiparamétrico es un modelo de regresión con un componente de dimensión finita e infinita.

Un componente de dimensión finita está atravesado por una lista de vectores (un vector es un objeto que tiene tanto magnitud como dirección). Los espacios bidimensionales y tridimensionales con los que tratamos en la geometría cotidiana son ejemplos de espacios de dimensión finita, pero también lo es un espacio hipotético de 4568 dimensiones. Los espacios de dimensión infinita son espacios que tienen un número infinito, y posiblemente mal definido , de dimensiones y posibilidades. No están abarcados por ninguna lista finita de vectores.

En contraste con los modelos paramétricos , que están bien definidos en el espacio de dimensión finita, y los modelos no paramétricos , donde todos los parámetros pueden abarcar un espacio infinito, un modelo semiparamétrico tiene un componente que es de dimensión finita (es decir, es fácil de investigar y comprender), y otro que es de dimensión infinita (es decir, más allá del alcance de los métodos estadísticos ordinarios).

En los proyectos de investigación y estadística que involucran modelos semiparamétricos, el énfasis casi siempre está en el componente paramétrico del modelo. Eso es porque esta es la parte que se presta bien a la investigación.

¿Por qué usar modelos semiparamétricos?

Con demasiada frecuencia, los modelos paramétricos, si bien son fáciles de entender y trabajar con ellos, no brindan una representación justa de lo que sucede en el mundo real. Los modelos no paramétricos pueden ser mejores representaciones, pero no se prestan bien al análisis. Un modelo semiparamétrico le permite tener lo mejor de ambos mundos: un modelo que es comprensible y puede manipularse mientras ofrece una representación justa del desorden que implica la vida real.

Ejemplos de modelos semiparamétricos

Un ejemplo de un modelo semiparamétrico es el modelo de riesgos proporcionales de Cox . Este modelo es muy útil en estudios del tiempo que queda antes de un final o falla; se usa cuando se investiga el tiempo que queda antes de que un paciente muera o antes de que se queme una bombilla. Se define como: Aquí x es lo que llamamos el vector covariable, y nuestros parámetros desconocidos son Β y λ ₀ (u) . Β es de dimensión finita y, a menudo, es objeto de investigación; λ ₀ (u) , por otro lado, es una función del tiempo desconocida y no negativa, y el espacio de posibilidades de λ ₀ (u) es infinito. Lo llamamos un ‘ parámetro molesto

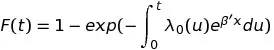
‘; un parámetro que no se puede omitir por completo en un tratamiento riguroso de un problema pero que no es de interés inmediato, generalmente porque es difícil o imposible de estudiar.

Los modelos de mezcla gaussiana son semiparamétricos. Paramétrico implica que el modelo proviene de una distribución conocida (que es en este caso, un conjunto de distribuciones normales ). Es semiparamétrico porque se pueden agregar al modelo más componentes, posiblemente de distribuciones desconocidas.

Referencias

Álgebra vectorial