Simulación Monte Carlo / Método

Actualizado el 26 de octubre de 2021, por Luis Benites.

1. ¿Qué es la simulación Monte Carlo?

La simulación de Monte Carlo (también llamada método de Monte Carlo o muestreo de Monte Carlo ) es una forma de tener en cuenta el riesgo en la toma de decisiones y el análisis cuantitativo. El método encuentra todos los resultados posibles de sus decisiones y evalúa el impacto del riesgo. Fue inventado durante el Proyecto Manhattan por John von Neumann y Stanislaw Ulam y llamado así por el tío de Ulem que disfrutaba jugando juegos de azar en Montecarlo, Mónaco.

La técnica utiliza métodos de muestreo estadístico intensivo que son tan complejos que generalmente solo se realizan con la ayuda de una computadora. El procedimiento es complejo por varias razones:

1. El modelo de entrada se simula cientos o miles de veces (o, a veces, cientos de miles de veces), donde cada simulación final es igualmente probable. El resultado es una distribución de probabilidad de posibles resultados. Esta podría ser una o muchas distribuciones diferentes, incluida la distribución normal, la distribución de chi-cuadrado , la distribución uniforme o una de las docenas de distribuciones de probabilidad diferentes .
2. Monte Carlo transforma números de un generador de números aleatorios, y las secuencias de estos números transformados se repetirán después de un cierto número de muestras . Si bien el error en el cálculo de las estadísticas (como la media ) será aceptable, los errores no desaparecerán por completo ni se volverán insignificantes. Esto viola el Teorema del Límite Central y la Ley de los Grandes Números (Fishman, 1996), dos teoremas que son la base de las estadísticas «habituales» con las que la mayoría de la gente se siente cómoda. Si su objetivo es la precisión absoluta, este método no es para usted, pero si está buscando números que estén «en el estadio de béisbol» con un error del 5-10% en el mejor de los casos, entonces esta puede ser una buena opción.

El método Monte Carlo te dice:

• Todos los eventos posibles que podrían o van a suceder,
• La probabilidad de cada resultado posible.

En lo que respecta al proyecto de Manhattan, uno de los posibles eventos que pudo haber ocurrido fue que la bomba atómica provocó una reacción en cadena que hizo estallar el mundo. La probabilidad se calculó como tan improbable que era imposible (dicho esto, ¡la simulación sí tuvo en cuenta la posibilidad!).

Volver arriba

2. Probabilidad cuantificada y usos en la vida real

La simulación de Monte Carlo devuelve una probabilidad cuantificada , lo que significa que le brinda escenarios con números que puede usar. Supongamos que su empresa quiere saber si la vida de las aves locales se verá afectada negativamente por la construcción de una nueva fábrica cerca de los humedales. Una probabilidad cuantificada sería «Si construimos la fábrica, hay un 30% de posibilidades de que la población de aves que anidan se vea afectada negativamente». Esto es más útil que una afirmación más general y calificada como “Si construimos la fábrica, la población de aves que anidan se verá afectada”.

Las simulaciones de Monte Carlo se utilizan en muchas áreas de la industria y la ciencia, que incluyen:

• Análisis de problemas de transferencia de calor por radiación (Wang et.al),
• Estimación de la transmisión de partículas a través de la materia (Biersack & Haggmark),
• Cálculo de la probabilidad de sobrecostos en grandes proyectos (McCabe),
• Prever dónde es probable que se muevan los precios de los valores (Boyle et. al),
• Analizar cómo se comportará una red o red eléctrica en diferentes escenarios. Por ejemplo, Sortomme et. al realizó simulaciones sobre cómo la carga de vehículos eléctricos afectará a la plataforma eléctrica en el futuro.
• Evaluación del riesgo de crédito o seguro (Gordy).
• Simulación de proteínas en biología (Earl et. al)

Volver arriba

3. Precisión

Si bien una simulación de Monte Carlo proporciona una buena precisión , es poco probable que alcance la marca «exacta» por varias razones:

1. Por lo general, se involucran grandes cantidades de datos.
2. Por lo general, hay varias incógnitas en el sistema.
3. Como es probabilístico (es decir, la aleatoriedad juega un papel en la predicción de eventos futuros), siempre habrá un margen de error relacionado con los resultados.

De hecho, puede ser bastante fácil ejecutar una simulación Monte Carlo “mala” (Brandimarte, 2014). Esto puede suceder por una variedad de razones, que incluyen:

• Uso de un modelo incorrecto o una distribución de probabilidad poco realista,
• Los factores de riesgo subyacentes no están completos (es decir, no los ha especificado lo suficientemente bien),
• La elección de Monte Carlo (que utiliza un modelo estocástico ) no se adapta a sus datos,
• El generador de números aleatorios elegido para el método no es lo suficientemente bueno,
• Errores informáticos, de los que quizás no tenga conocimiento si su área de especialización es la estadística (en lugar de la programación).

Volver arriba

4. Ejemplo simple de cómo funciona Monte Carlo

Ejemplo 1. Probabilidades de Blackjack

Un Blackjack en cartas consiste en un As y una carta de diez puntos.

Digamos que desea encontrar la probabilidad de obtener un blackjack (un «21» en las cartas). Los ases valen 11 puntos y las siguientes cartas valen diez puntos: Jota, Reina, Rey. Podrías anotar todas las posibilidades :

• Diez de tréboles / As de tréboles
• Jota de tréboles / As de tréboles
• Reina de tréboles / As de tréboles
• Jota de tréboles / As de tréboles…

Si escribiera todas las combinaciones posibles de cartas (incluidas todas las combinaciones de dos cartas que no suman 21), encontraría que la probabilidad de obtener un Blackjack es de aproximadamente 1:21. En otras palabras, la probabilidad de obtener obtener un blackjack es uno en 21 manos. Con números pequeños, como una baraja de cartas, calcular su espacio de muestra (es decir, todos los resultados posibles) es bastante simple y no toma mucho tiempo. Pero si tener una mayor cantidad de entradas, digamos, miles de tarjetas, luego calcular un espacio de muestra usando un método probabilístico como este se vuelve difícil de manejar.Ingrese al método de Monte Carlo.

Otra forma de calcular la probabilidad de obtener un Blackjack es elegir dos cartas un número determinado de veces (por ejemplo, cien veces) y registrar los resultados. Cuantas más veces tome una muestra de dos tarjetas, más se acercará a la cifra «real» de 1:21. Por ejemplo, si eliges dos cartas mil veces, probablemente te acerques mucho a 1:21; Si elige dos cartas una docena de veces, es probable que no se acerque en absoluto; es posible que tenga una racha de «suerte» o que no obtenga «21» en absoluto. Básicamente, así es como funcionan las simulaciones de Monte Carlo. En lugar de escribir el espacio muestral (que es lo que hicimos en la primera parte de este ejemplo), Monte Carlo muestrea y ubica el resultado más probable , creando un modelo estocástico . El hecho de que Monte Carlo use un sorteo muy simple (en este ejemplo, dos cartas) y lo repita una y otra vez, es la razón por la cual el método a veces se llama el Método de Pruebas Estadísticas.
Volver arriba

5. El método de división

El método de división es una simulación de Monte Carlo para eventos raros o para el muestreo de datos de alta dimensión . El programa toma un escenario complejo y lo «divide» en partes fáciles de calcular. En un nivel básico, el programa aumenta la probabilidad de que ocurra el evento para que se pueda encontrar una distribución de probabilidad.

6. EJEMPLO DE SOFTWARE Y MATLAB

Se ha desarrollado una amplia variedad de software para ejecutar simulaciones Monte Carlo. Éstos incluyen:

• Lenguajes de programación de propósito general (p. ej., C++, Java o Visual Basic),
• Complementos de hojas de cálculo (por ejemplo, Excel),
• Paquetes de software estadístico (por ejemplo, R, MATLAB, R y SPSS).
• Editores gráficos (por ejemplo, Simulink y Arena20).

Ejemplo 2 de MATLAB: recopilación de cartas

Cuando viajé de mochilero por los Estados Unidos por primera vez en la década de 1980, McDonald’s estaba realizando una promoción en la que tenías que recolectar pequeños pedazos de Monopoly de papel pegados a los lados de las papas fritas y bebidas Super Size. A pesar de saber que las probabilidades no estaban a mi favor, mi yo más joven no pudo resistirse a comprar comidas de filete de pescado de gran tamaño para tratar de ganar. Creo que lo que más gané fue un gran alevín, pero sirve para ilustrar el poder de estas técnicas de marketing.

Por lo general, el juego se trata realmente de quién tiene la suerte de obtener las piezas raras . En 2016, las piezas raras incluyeron Mayfair por £ 100,000 en efectivo (Reino Unido) o Boardwalk por $ 1,000,000 (EE. UU.). Para este código de ejemplo, se supone que existe la misma posibilidad de obtener todas las piezas de juego.

> nLetras = 9; %BIGMACFRY
> nTrials = 10000;
> for i=1:nTrials
> éxito = 0;
> nTries(i) = 0;
> para j=1:nLetras
> BIGMACFRY(j)=0; %reset letra no lograda
> final
> mientras éxito == 0
> nTries(i) = nTries(i)+1; %Cª. contar
> comprar = 1+piso(nLetras*rand); %letra obtenida
> BIGMACFRY(comprar) = 1;
> si suma(BIGMACFRY)==nLetras
> exito = 1;
> final
> final
> final
> hist(nTries)

(Código MATLAB modificado de Shonkwiler & Mendivil, “Explorations in Monte Carlo Methods”)

7. Histograma

La histograma es una forma popular de mostrar los resultados de las simulaciones de Monte Carlo. El siguiente histograma muestra los resultados de la simulación de piezas de Monopoly anterior. El histograma revela un par de resultados sorprendentes:

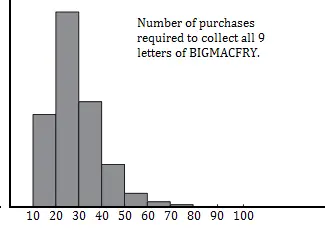
1. Podría tomar 100 compras para obtener las 9 piezas.
2. El número de compras alcanza su punto máximo después del mínimo (que, si tienes una racha de suerte, es 9); el modelo entonces decrece exponencialmente.

Volver arriba

Referencias:

Biersack y Haggmark. Un programa informático Monte Carlo para el transporte de iones energéticos en objetivos amorfos. Instrumentos y Métodos Nucleares. Volumen 174, números 1 y 2, 1 de agosto de 1980, páginas 257-269. Recuperado el 26 de agosto de 2017 de: Science Direct .
Boyle et. Alabama. Métodos de Monte Carlo para la fijación de precios de valores. Journal of Economic Dynamics and Control
Volumen 21, números 8 y 9, 29 de junio de 1997, páginas 1267-1321. Recuperado el 26 de agosto de 2017 de: http://www.sciencedirect.com/science/article/pii/S0165188997000286
Brandimarte, P. (2014). Manual de simulación Monte Carlo: aplicaciones en ingeniería financiera, gestión de riesgos y economía. Wiley.
Earl et. Alabama. Simulación del Monte Carlo. Modelado Molecular de Proteínas pp 25-36. Recuperado el 26 de agosto de 217 de: https://link.springer.com/protocol/10.1007/978-1-59745-177-2_2
Fishman, G. (1996). Montecarlo . Springer Science & Business Media.
Gordi. Una anatomía comparativa de los modelos de riesgo de crédito. Journal of Banking & Finance
Volumen 24, números 1 y 2, enero de 2000, páginas 119-149. Recuperado en agosto de 2017 de: http://www.sciencedirect.com/science/article/pii/S0378426699000540
McCabe, B. Ingeniería de construcción y gestión de proyectos III: simulación Monte Carlo para riesgos de cronograma. WSC ’03 Actas de la 35.ª conferencia sobre simulación invernal: impulsando la innovación. Páginas 1561-1565. Recuperado el 26 de agosto de 2017 de: Biblioteca Digital ACM .
Shonkwiler y Mendivil. Exploraciones en Métodos Monte Carlo. 2009. Springer.
Sortomme et. Alabama. Carga coordinada de vehículos eléctricos híbridos enchufables para minimizar las pérdidas del sistema de distribución. Transacciones IEEE en Smart Grid . Marzo de 2011. Volumen: 2 Edición: 1
Wang et. Alabama. Simulación Monte Carlo de transferencia de calor radiativo e interacciones de turbulencia en llamas de chorro de metano/aire. Revista de Espectroscopía Cuantitativa y Transferencia Radiativa.
Volumen 109, Número 2, enero de 2008, páginas 269-279. Recuperado el 26 de agosto de 2017 de: http://www.sciencedirect.com/science/article/pii/S0022407307002464