Correlación policórica

Actualizado el 21 de agosto de 2021, por Luis Benites.

¿Qué es la correlación policórica?

La correlación policórica mide el acuerdo entre múltiples evaluadores para variables ordinales (a veces llamados datos de «categoría ordenada»). Las variables ordinales se pueden colocar en orden, pero no se pueden dividir ni multiplicar. Por ejemplo: el nivel de depresión de una persona, su nivel de desacuerdo o acuerdo, o cuánto valoran las posesiones.

Cálculo de la correlación policórica

El coeficiente policórico fue reconocido en la historia por ser difícil de calcular e implicaba cálculo . El término «correlación policórica» ​​en realidad se refiere a un método de tabla de cálculo previo que utiliza la serie policórica. Las tablas, desarrolladas por Karl Pearson , facilitaron un poco el proceso, pero ahora es inusual realizar el cálculo a mano; Casi siempre se utiliza software y los cálculos se realizan utilizando el método de máxima verosimilitud, no tablas. La mayoría del software estadístico tiene una opción para encontrar el coeficiente. La entrada suele ser una tabla de contingencia n*m .

• En SAS, use el procedimiento CORR ( que se encuentra aquí ).
• SPSS no tiene un procedimiento incorporado, pero tiene un comando de extensión (SPSS HETCOR) que puede descargar desde la comunidad de SPSS . (Haga clic en «Descargas para IBM SPSS Statistics», luego en «Comandos de extensión» que figuran en «Extensiones, herramientas y utilidades». Escriba HETCOR en el cuadro de búsqueda (arriba a la izquierda) y luego haga clic en SPSSINC_HETCOR en la lista de resultados.

Si desea calcular el coeficiente a mano, Mangal (2010) ofrece la siguiente fórmula como una buena aproximación a la correlación tetracórica :

cos(180/(√AD/BC)+1)

Donde (AD/BC) es la razón de probabilidades .

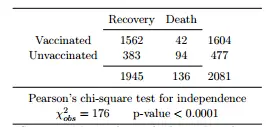
Tabla de contingencia para los datos de recuperación de la viruela de Karl Pearson.

Interpretación de los resultados

El policlórico es similar a la correlación lineal ; El coeficiente está entre 0 y 1, donde 0 es sin relación y 0 es una relación perfecta.

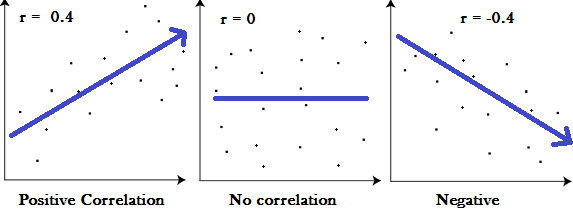
Gráficos que muestran una correlación de -1, 0 y +1.

Referencia :
Mangal, SK Estadísticas en Psicología y Educación. Segunda edicion. 2010.
Pearson, K. (1900). Contribuciones matemáticas a la teoría de la evolución. VIII. Sobre la correlación de caracteres no medibles cuantitativamente. Filosofía Trans. R. Soc. largo Ser. Una Matemática. física Ing. Sci., 195, 1–47. Disponible aquí .