Contenido de este artículo
- 0
- 0
- 0
- 0
Actualizado el 12 de abril de 2022, por Dereck Amesquita.
El error estándar de la estimación es una forma de medir la precisión de las predicciones realizadas por un modelo de regresión.
Denominado a menudo σ est , se calcula como:
σ est = √ Σ (y – ŷ) 2 / n
dónde:
- y: el valor observado
- ŷ: el valor predicho
- n: el número total de observaciones
El error estándar de la estimación nos da una idea de qué tan bien se ajusta un modelo de regresión a un conjunto de datos. En particular:
- Cuanto menor sea el valor, mejor será el ajuste.
- Cuanto mayor sea el valor, peor será el ajuste.
Para un modelo de regresión que tiene un pequeño error estándar de la estimación, los puntos de datos se empaquetarán estrechamente alrededor de la línea de regresión estimada:
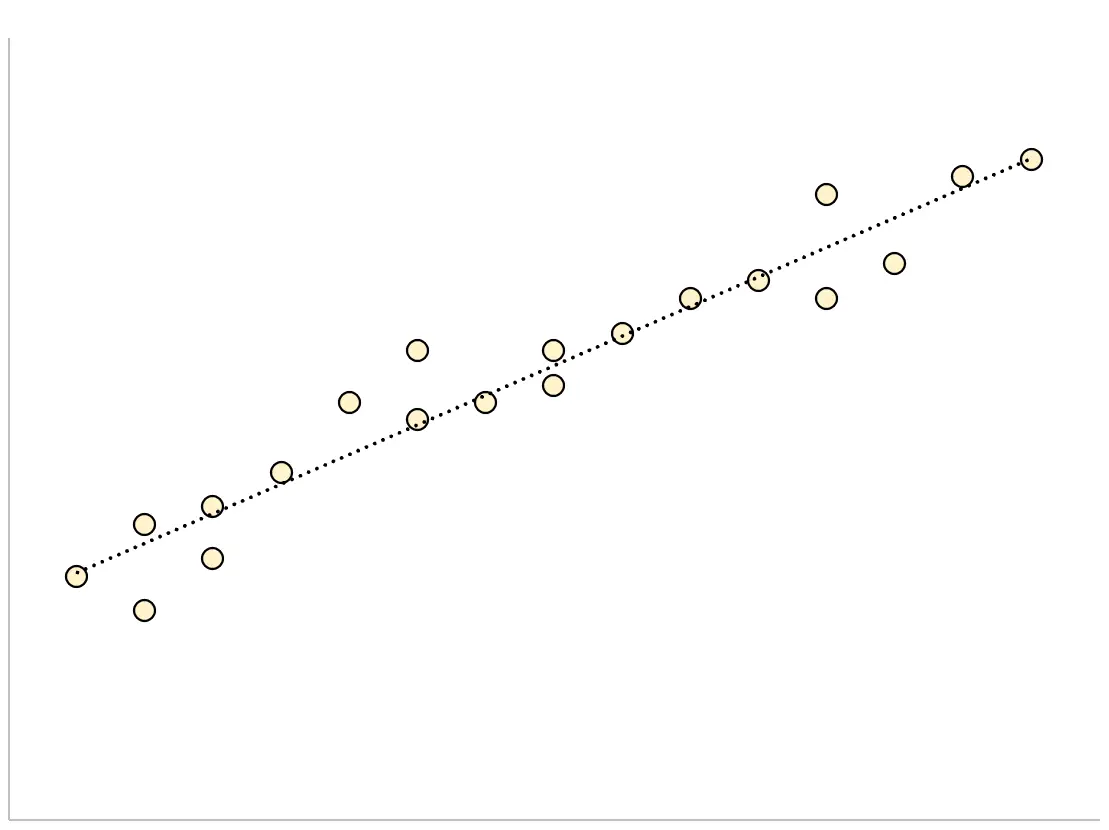
Por el contrario, para un modelo de regresión que tiene un gran error estándar de la estimación, los puntos de datos estarán más dispersos alrededor de la línea de regresión:
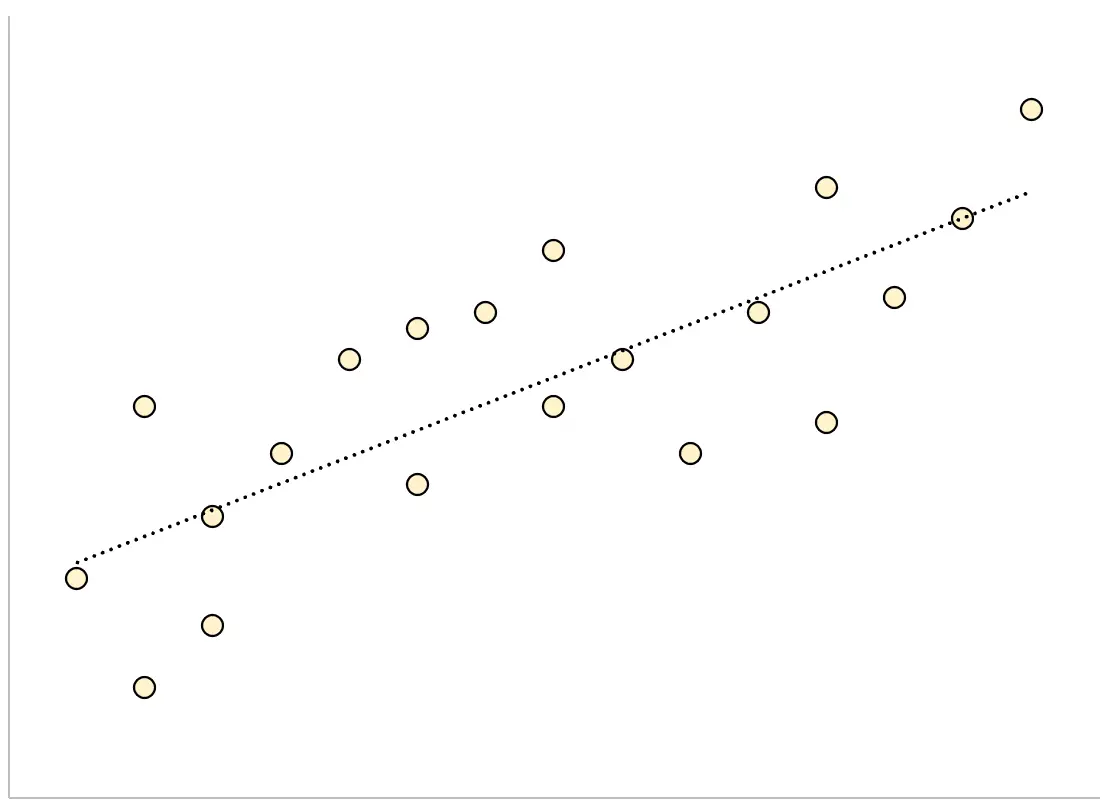
El siguiente ejemplo muestra cómo calcular e interpretar el error estándar de la estimación para un modelo de regresión en Excel.
Ejemplo: error estándar de la estimación en Excel
Utilice los siguientes pasos para calcular el error estándar de la estimación para un modelo de regresión en Excel.
Paso 1: ingrese los datos al Excel
Primero, ingrese los valores para el conjunto de datos:
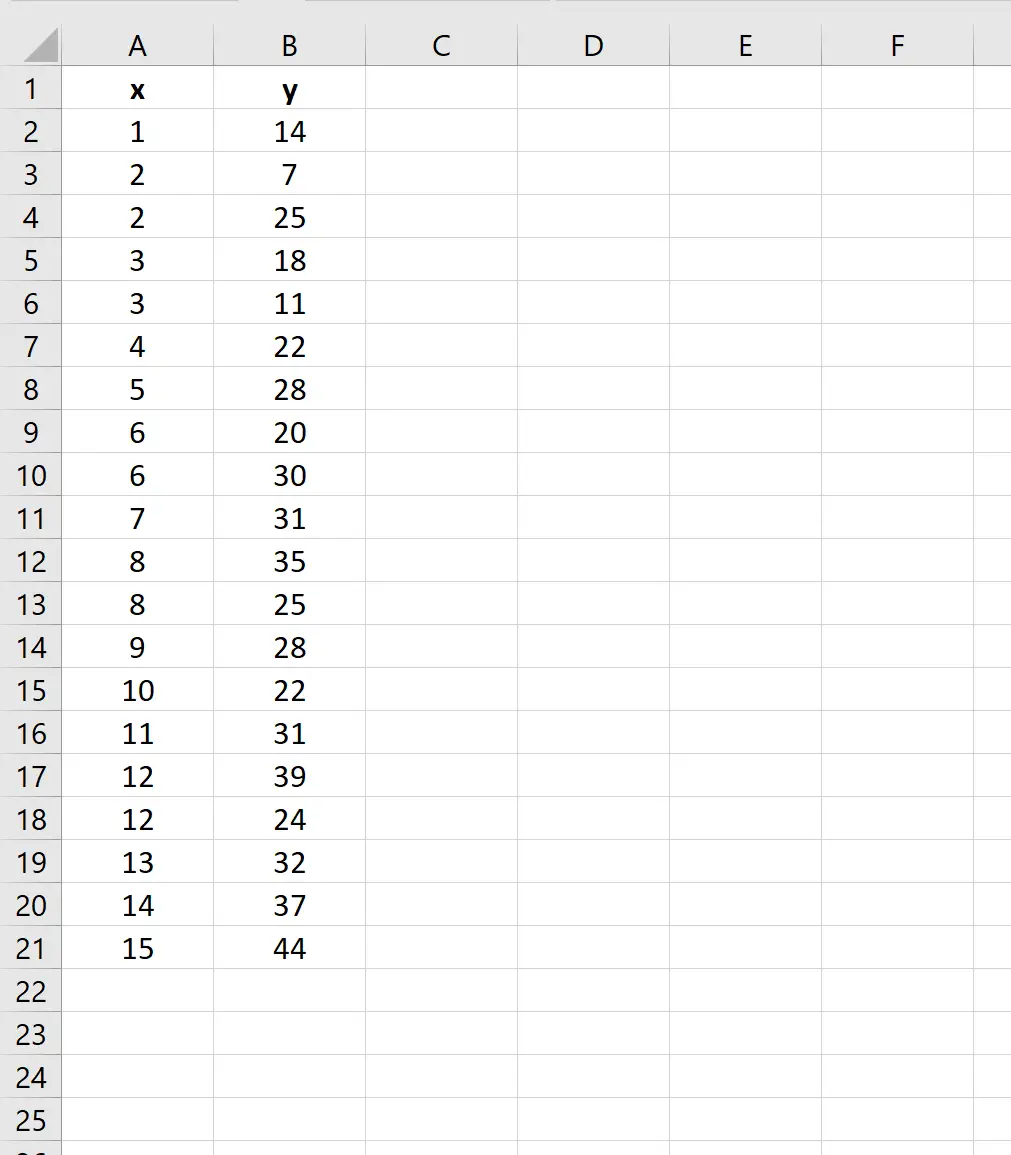
Paso 2: realizar una regresión lineal
A continuación, haga clic en la pestaña Datos a lo largo de la cinta superior. Luego haga clic en la opción Análisis de datos dentro del grupo Analizar .
Si no ve esta opción, primero debe cargar Analysis ToolPak .
En la nueva ventana que aparece, haga clic en Regresión y luego haga clic en Aceptar .
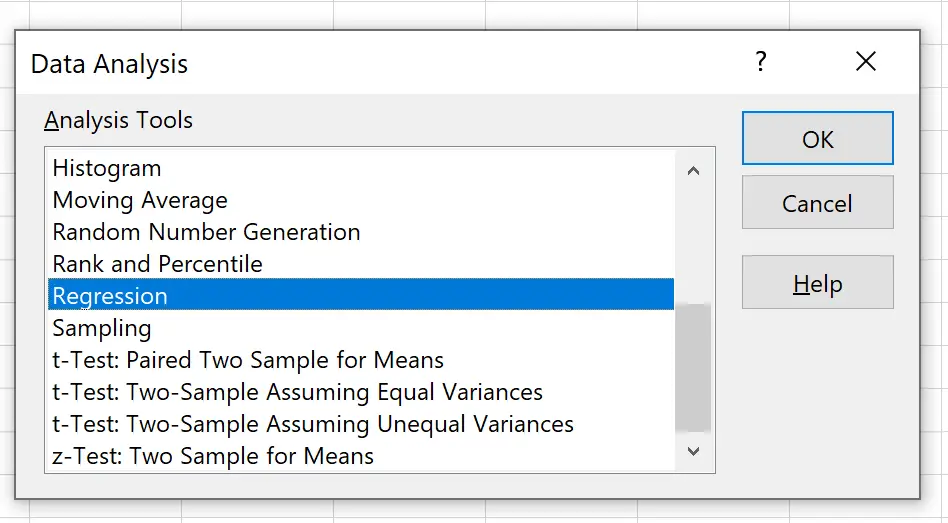
En la nueva ventana que aparece, complete la siguiente información:
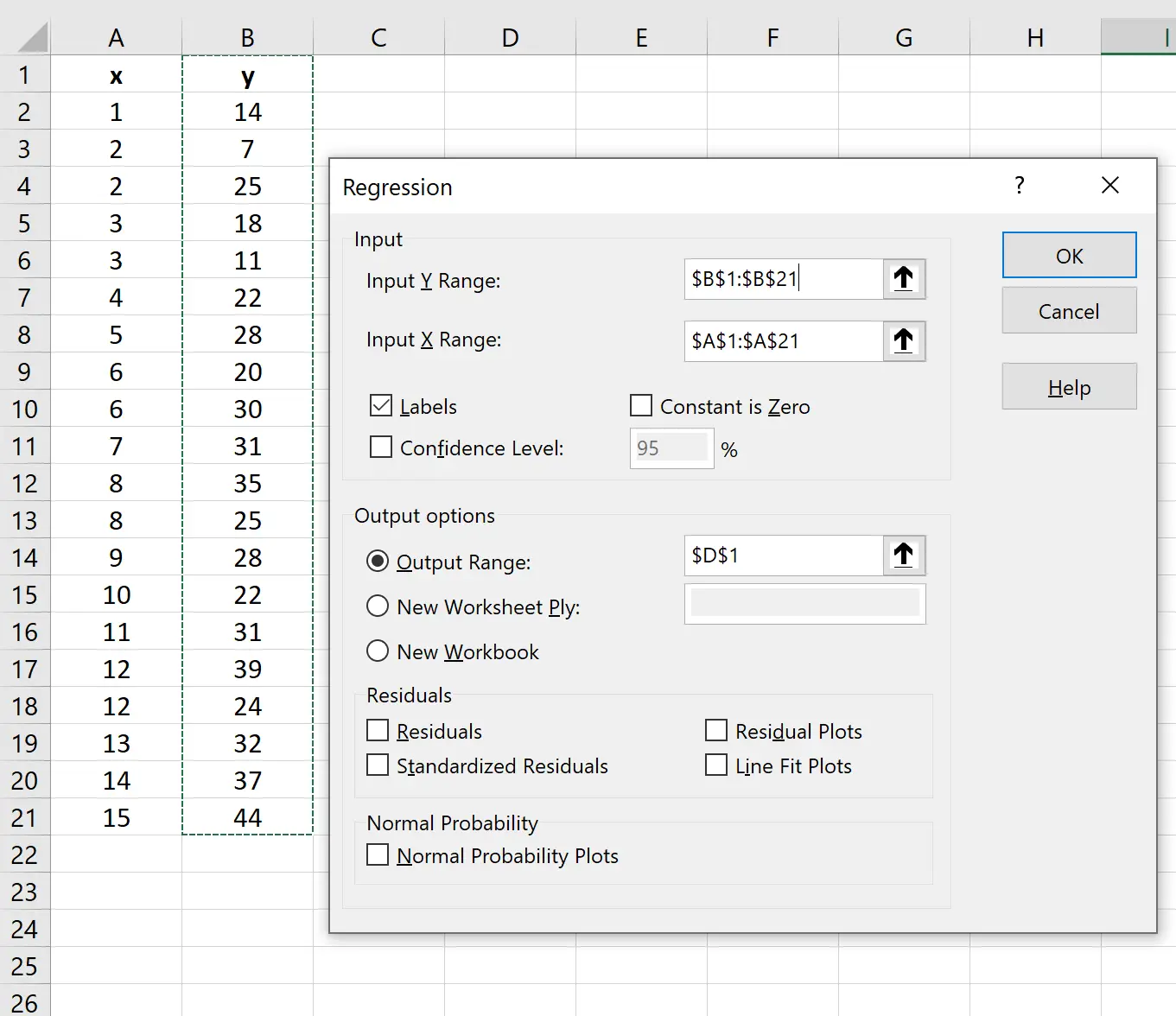
Una vez que haga clic en Aceptar , aparecerá el resultado de la regresión:
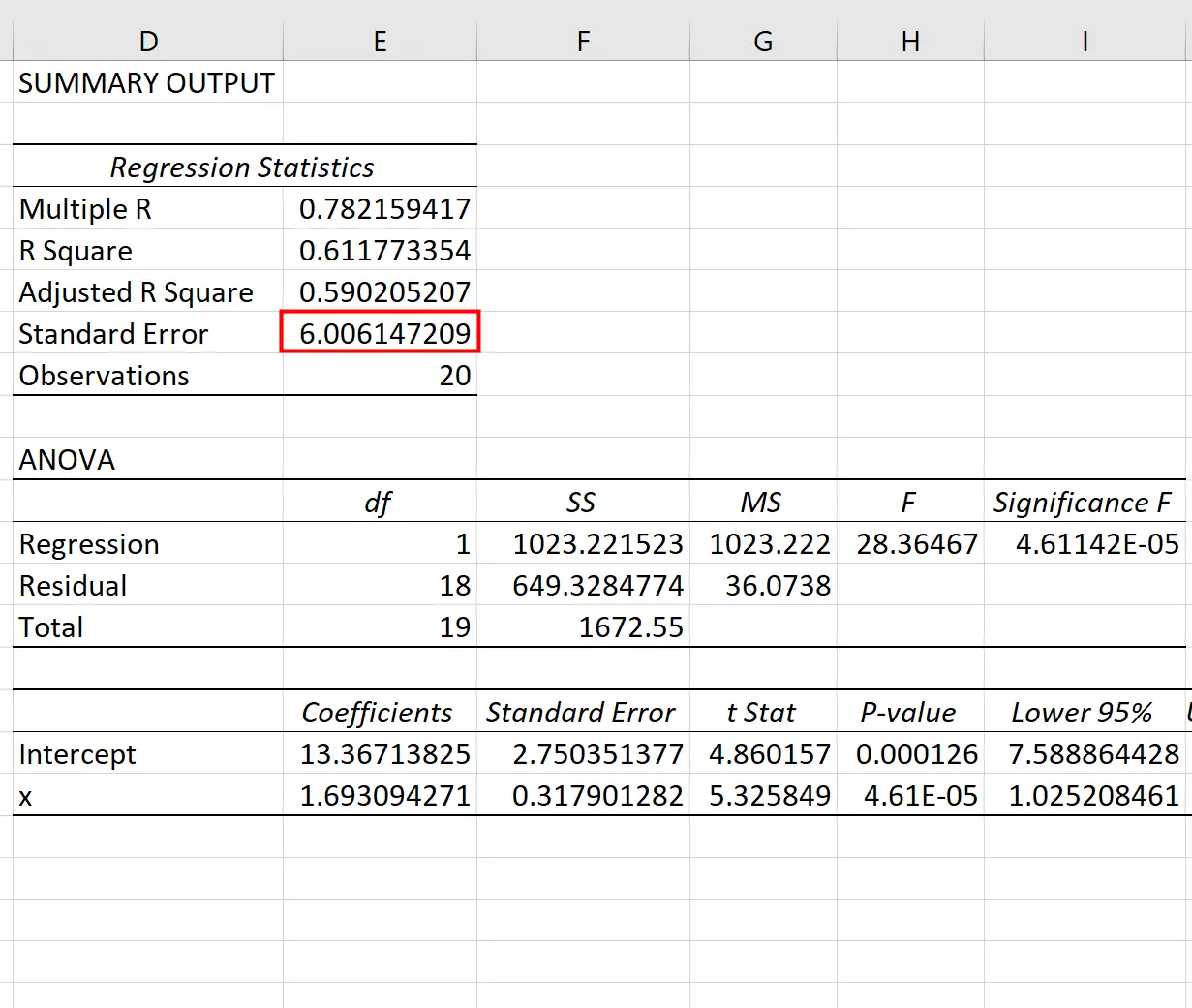
Podemos usar los coeficientes de la tabla de regresión para construir la ecuación de regresión estimada:
ŷ = 13,367 + 1,693 (x)
Y podemos ver que el error estándar de la estimación para este modelo de regresión resulta ser 6,006 . En términos simples, esto nos dice que el punto de datos promedio cae 6.006 unidades de la línea de regresión.
Podemos utilizar la ecuación de regresión estimada y el error estándar de la estimación para construir un intervalo de confianza del 95% para el valor predicho de un determinado punto de datos.
Por ejemplo, suponga que x es igual a 10. Usando la ecuación de regresión estimada, predeciríamos que y sería igual a:
ŷ = 13,367 + 1,693 * (10) = 30,297
Y podemos obtener el intervalo de confianza del 95% para esta estimación utilizando la siguiente fórmula:
- IC del 95% = [ŷ – 1,96 * σ est , ŷ + 1,96 * σ est ]
Para nuestro ejemplo, el intervalo de confianza del 95% se calcularía como:
- IC del 95% = [ŷ – 1,96 * σ est , ŷ + 1,96 * σ est ]
- IC del 95% = [30,297 – 1,96 * 6,006, 30,297 + 1,96 * 6,006]
- IC del 95% = [18,525, 42,069]
Recursos adicionales
Cómo realizar una regresión lineal simple en Excel
Cómo realizar una regresión lineal múltiple en Excel
Cómo crear una gráfica residual en Excel
- https://r-project.org
- https://www.python.org/
- https://www.stata.com/
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo:
