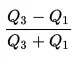Actualizado por ultima vez el 1 de noviembre de 2021, por Luis Benites.
¿Qué es el rango semiintercuartílico?
El rango semiintercuartil (SIR) (también llamado desviación del cuartil ) es una medida de dispersión . Te dice algo sobre cómo se dispersan los datos alrededor de un punto central (generalmente la media ).
El SIR es la mitad del rango intercuartílico .
Cómo calcular el rango semiintercuartílico/la desviación del cuartil
Como el SIR es la mitad del rango intercuartil, todo lo que necesitas hacer es encontrar el IQR y luego dividir tu respuesta por 2.
Otra forma es usar la fórmula de desviación del cuartil : Nota : es posible que vea la fórmula QD = 1/2 (Q 3 – Q 1 ). Algebraicamente son lo mismo.
![]()
Desglosando la fórmula anterior:
Paso 1: Encuentra el primer cuartil, Q 1 . Si te dan Q 1 en la pregunta, genial. Si no, tienes varias opciones, que incluyen:
- Usa una calculadora, como esta . Introduce tus números y haz clic en el botón azul. Q 1 es igual al percentil 25 que figura en los resultados.
- Siga estas instrucciones para encontrar el rango intercuartil a mano (parte del proceso es encontrar cuartiles ).
Paso 2: Encuentra el tercer cuartil, Q 3 . Si te dan Q 3 en la pregunta, genial. De lo contrario, use una de las opciones enumeradas en el Paso 1. Si elige usar la calculadora, Q 3 es igual al percentil 75.
Paso 3: Resta el Paso 1 del Paso 2.
Paso 4: Dividir por 2.
Ejemplo
Pregunta : encuentre la desviación del cuartil para el siguiente conjunto de datos:
{490, 540, 590, 600, 620, 650, 680, 770, 830, 840, 890, 900}
Paso 1: Encuentra el primer cuartil, Q 1 .
Esta es la mediana de la mitad inferior del conjunto {490, 540, 590, 600, 620, 650}.
Q 1 = (590 + 600) / 2 = 595.
Paso 2: Encuentra el tercer cuartil, Q 3 .
Esta es la mediana de la mitad superior del conjunto {680, 770, 830, 840, 890, 900}.
Q 3 = (830 + 840) / 2 = 835.
Paso 3: Resta el Paso 1 del Paso 2.
835 – 595 = 240.
Paso 4: Divide por 2. 240 / 2 = 120
La desviación del cuartil para este conjunto de datos es 12.
Coeficiente de desviación del cuartil
El coeficiente de desviación del cuartil (a veces denominado coeficiente de dispersión del cuartil) le permite comparar la dispersión de dos o más conjuntos de datos. La fórmula es: si un conjunto de datos tiene un coeficiente de desviación de cuartil mayor que otro conjunto, entonces la dispersión intercuartil de ese conjunto de datos es mayor.