Actualizado por ultima vez el 31 de octubre de 2021, por Luis Benites.
¿Qué es una distribución de Lindley?
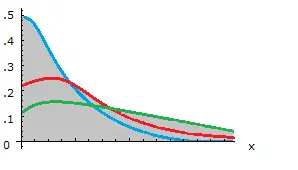Una distribución de Lindley es una forma de describir la vida útil de un proceso o dispositivo. Se puede utilizar en una amplia variedad de campos, incluida la biología, la ingeniería y la medicina. Ghitany et. al (2011) afirman que es especialmente útil para modelar en estudios de mortalidad. El parámetro de forma , θ es un número real positivo y puede dar como resultado una distribución unimodal o monótona decreciente (es decir, consistentemente decreciente). Esta distribución tiene colas delgadas porque la distribución decrece exponencialmente para valores grandes de x. El término «Distribución Exponencial de Lindley» se usa a menudo para referirse a la forma generalizada de la distribución.
PDF y CDF
La función de densidad de probabilidad de una variable aleatoria X en una distribución de Lindley con parámetro θ es:
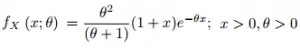
PDF para el Lindley.
La función de distribución acumulada para la función de un parámetro es:
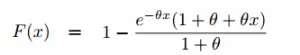
Tipos
En la literatura académica se han descrito muchas formas de distribución, que incluyen:
- Una forma de dos parámetros (Shanker et. al),
- Una forma ponderada de dos parámetros (Ghitany et ‘al),
- Un Poisson-Lindley generalizado (Mahmoudi et. al.),
- Una distribución extendida (EL) (Bakouch et. al),
- Una distribución geométrica exponencial (Adankis y Loukas).
- La distribución geométrica de Lindley transmutada (Merovci y Elbatal)
Momentos
Momentos para la distribución de un parámetro (de Shanker et. al): tenga en cuenta que estos momentos solo son válidos para la forma de un parámetro. Otros parámetros tendrán momentos diferentes . Por ejemplo, puede encontrar momentos para la distribución Lindley-Geometric transmutada con lo siguiente: Si X tiene T LG (θ, x) ,φ = (θ, p,λ) entonces el momento r-ésimo de X viene dado por (de Merovci y Elbatal): Dónde y
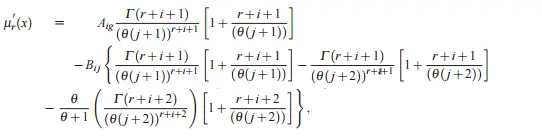
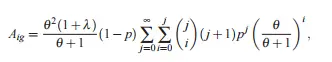
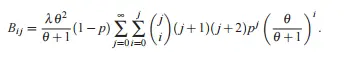
Distribuciones relacionadas
Distribuciones relacionadas que modelan tiempos de vida:
- Distribución Exponencial . Según Shanker et. al (1995), una ventaja de la distribución de Lindely en comparación con la distribución exponencial es que «… la distribución exponencial tiene una tasa de riesgo y una función de vida residual media constantes, mientras que la distribución de Lindley tiene una tasa de riesgo creciente y una función de vida residual media decreciente».
- Distribución gamma ,
- Distribución Weibull .
Referencias :
Adamidis K. y Loukas S., (1998) Una distribución de por vida con una tasa de falla decreciente, Statistics and Probability Letters, Vol(39), 35-42.
Bakouch HS, Al-Zahrani BM, Al-Shomrani AA, Marchi VA y Louzada F., (2012)
An extended LD, Journal of the Korean Statistical Society, Vol(41), 75-85.
Bhati, D. y Malik, A., (2014), Sobre la distribución exponencial de Lindley: propiedades y aplicación. Recuperado el 24/8/2016 de https://arxiv.org/pdf/1406.3106.pdf.
Ghitany ME, Alqallaf F., Al-Mutairi DK y Husain HA, (2011) Una distribución de Lindley ponderada de dos parámetros y sus aplicaciones a datos de supervivencia, Matemáticas y computadoras en simulación , vol. (81), núm. 6,1190-1201.
Mahmoudi E. y Zakerzadeh H., (2010) Generalized Poisson Lindley, Communications in Statistics: Theory and Methods, Vol (39), 1785-1798.
Merovci, F. y Elbatal, I. (2014) Distribución geométrica de Lindley transmutada y sus aplicaciones. Journal of Statistics Applications and Probability, 3, No. 1, 77-91 (20). Recuperado el 24/8/2016 de http://naturalspublishing.com/files/published/e69vpy514e5z24.pdf.
Shanker R., Sharma S. y Shanker R., (2013) Un Lindley de dos parámetros para
modelar datos de tiempos de espera y supervivencia, Matemáticas aplicadas, vol (4), 363-368. Recuperado el 24/08/2016 de aquí .
Shanker et. al (2015). Sobre el modelado de datos de vidas utilizando distribuciones exponenciales y de Lindley. Revista internacional de biometría y bioestadística. Volumen 2 Número 5.
