Distribución Arfwedson

Actualizado el 19 de abril de 2022, por Luis Benites.

La distribución de Arfwedson es una distribución de probabilidad discreta para un problema de muestreo de urnas para dibujos sin reemplazo. En concreto, aborda el problema “Una urna contiene N bolas numeradas. Hacemos n sorteos reemplazando la bola en la urna cada vez. ¿Cuál es la probabilidad de obtener v bolas diferentes? [1].
La distribución ha sido conocida por muchos nombres, incluyendo:

• La distribución de recolección de cupones, porque describe la probabilidad de que una persona con n cupones seleccionados al azar tenga al menos una de cada una de las k variedades igualmente probables [2].
• La distribución de ocupación clásica [3].
• Distribución de Stirling2, debido a la presencia de los números de Stirling de segunda especie [4].
• Copa Dixie [5].
• Stevens-Craig [6, 7].
• Fórmula de distribución de Arfwedson.

Hay varias fórmulas en la literatura, dependiendo de si el problema se aproxima al número de contenedores ocupados o al número de contenedores desocupados, lo que invierte la función de masa de probabilidad . Como ejemplo, Haight enumera la distribución de Arfwedson como [8]

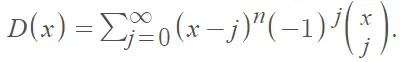
Arfwedson [1] proporciona el valor esperado en su artículo de 1951 como

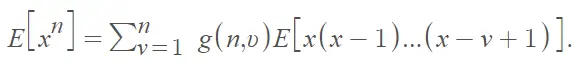
Donde los números g(n, ν) son números de segunda clase de Stirling. Una función generadora para estos está dada por

(ej. – 1) v

Sin embargo, Afrwedson ofrece otra fórmula (más complicada) como alternativa.

La función generadora de probabilidad de la distribución de Arfwedson es [1]:

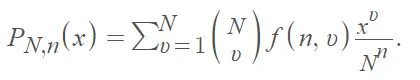
¡Que es igual al coeficiente de yn/n! en el desarrollo de esta siguiente expresión (obtenida a través de la integración ):

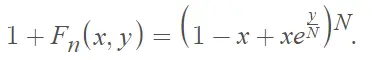
Referencias
[1] G. Arfwedson, Una distribución de probabilidad relacionada con los números de segunda clase de Stirling. Skand. Aktuaretidskr. 34 (1951), 121–132.

[2] David, FN y Barton, DE (1962). Posibilidad combinatoria, Londres: Griffin. [1.1.3, 10.2, 10.3, 10.4.1, 10.5, 10.6.1]

[3] O’Neill, B. (2019). La Distribución de Ocupación Clásica: Cómputo y Aproximación. El Estadístico Americano. norte, DOI: 10.1080/00031305.2019.1699445

[4] Williamson, PP, Mays, DP, Abay Asmerom, G. y Yang, Y. (2009), “Revisiting the Classical Occupancy Problem”, The American Statistician, 63, 356–360. [1,2,3]

[5] Johnson, NL y Kotz, S. (1977). Modelos de urnas y su aplicación, Nueva York: Wiley. [3.10, 4.2.1, 5.1, 10.4.1, 10.4.2, 11.2.19]

[6] Stevens, WL (1937). Importancia de la agrupación, Annals of Eugenics, Londres, 8, 57–60. [10.1, 10.4.1]

[7] Craig, CC (1953). Sobre la utilización de especímenes marcados en la estimación de poblaciones de insectos voladores, Biometrika, 40, 170–176. [10.1, 10.4.1]

[8] Haight, F. (1958). Índice de las Distribuciones de Estadísticas Matemáticas. Informe de la Oficina Nacional de Normas.