Actualizado por ultima vez el 15 de abril de 2022, por Luis Benites.
La distribución g y h (una combinación de la distribución g y la distribución h*) se utiliza en el modelado estadístico como una alternativa para los mínimos cuadrados ordinarios . Desarrollado por Tukey en 1977, rara vez se usa quizás porque no tiene una solución de forma cerrada para una función de densidad de probabilidad (PDF) . Turley (nd) afirma que como la distribución es tan difícil de calcular, tiene muy poca utilidad práctica . Sin embargo, a veces se utiliza como modelo para una distribución de gravedad.
Cálculo de los parámetros de distribución G-y-H
Los parámetros de la distribución g-y-h solo pueden calcularse por métodos indirectos como los basados en estadísticas de orden Dutta y Babbel (2005) o método de momentos / estimación de máxima verosimilitud Turley, P (nd).
La distribución g-and-h se puede definir por sus momentos , aunque requiere algunos cálculos pesados . El alcance de esto va más allá de este artículo, pero los detalles de la derivación de los primeros momentos se pueden encontrar en Cruz et. Aspectos fundamentales del riesgo operativo y análisis de seguros de al : un manual (págs. 318-319).
Algunas fórmulas están disponibles para variables aleatorias muy particulares . Por ejemplo, Chaudhuri y Ghosh ofrecen la siguiente fórmula para la distribución g-y-h para una variable aleatoria normal univariante Y g,h , definida por una transformación Z : Donde:
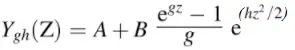
- A y B son parámetros de escala ,
- g y h controlan la asimetría y la curtosis .
* Tanto la distribución g como la distribución h pueden derivarse de la ecuación anterior. La distribución g se obtiene cuando h = 0 en la ecuación anterior. Corresponde a una distribución LogNormal escalada cuando g es una constante.
La distribución h se obtiene cuando g=0 en la ecuación.
Referencias:
Chaudhuri, A. & Ghosh, S. Obtenido el 8 de julio de 2017 de: Modelado cuantitativo del riesgo operativo en finanzas y banca usando la teoría de la posibilidad https://books.google.com/books?id=HMXYCgAAQBAJ&pg=PA29&dq=g- and-h+distribution&hl=en&sa=X&ved=0ahUKEwjJ76v76vnUAhWB6oMKHT7_A2AQ6AEIJDAA#v=snippet&q=g-and-h%20distribution&f=false
Dutta, KK y DF Babel (2002). Extracción de Información Probabilística de los Precios de Opciones de Tasa de Interés: Prueba de Supuestos Distributivos. El Diario de Negocios 78(3), 841-870.
Tukey, JW (1977). Análisis exploratorio de datos. Reading, MA: Addison-Wesley
Turley, P. Solo unos momentos más: la distribución g-and-h. Recuperado el 8 de julio de 2017 de: https://www.researchgate.

