Gráficos QQ: definición simple y ejemplo

Actualizado el 15 de abril de 2022, por Luis Benites.

Es posible que desee leer este artículo primero: ¿Qué es un cuantil ?

¿Qué es un gráfico QQ?

Los gráficos QQ (gráficos de cuantiles y cuantiles) son gráficos de dos cuantiles uno contra el otro. Un cuantil es una fracción donde ciertos valores caen por debajo de ese cuantil. Por ejemplo, la mediana es un cuantil en el que el 50 % de los datos se encuentran por debajo de ese punto y el 50 % por encima. El propósito de las gráficas QQ es averiguar si dos conjuntos de datos provienen de la misma distribución. Se traza un ángulo de 45 grados en el gráfico QQ; si los dos conjuntos de datos provienen de una distribución común, los puntos caerán en esa línea de referencia.

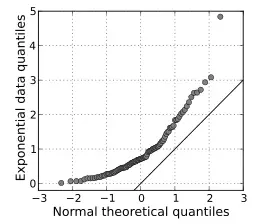
Gráfico AQQ que muestra la línea de referencia de 45 grados. Imagen: skbkekas|Wikimedia Commons.

La imagen de arriba muestra los cuantiles de una distribución normal teórica en el eje horizontal. Se está comparando con un conjunto de datos en el eje y. Este tipo particular de gráfica QQ se denomina gráfica cuantil-cuantil normal (QQ). Los puntos no están agrupados en la línea de 45 grados y, de hecho, siguen una curva, lo que sugiere que los datos de la muestra no tienen una distribución normal.

Cómo hacer un gráfico QQ

Ejemplo de pregunta: ¿Los siguientes valores provienen de una distribución normal?
7.19, 6.31, 5.89, 4.5, 3.77, 4.25, 5.19, 5.79, 6.79.

Paso 1: ordena los artículos de menor a mayor .

• 3.77
• 4.25
• 4.50
• 5.19
• 5.89
• 5.79
• 6.31
• 6.79
• 7.19

Paso 2: Dibujar una curva de distribución normal. Divide la curva en n+1 segmentos. Tenemos 9 valores, así que divide la curva en 10 áreas de igual tamaño. Para este ejemplo, cada segmento es el 10 % del área (porque 100 % / 10 = 10 %). Paso 3: Encuentre el valor z (punto de corte) para cada segmento en el Paso 3. Estos segmentos son áreas , así que consulte una tabla z (o use software) para obtener un valor z para cada segmento. Los valores z son:

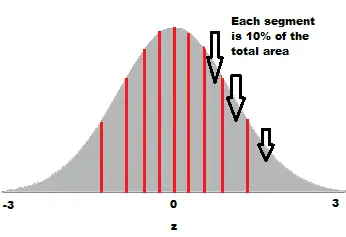
• 10% = -1.28
• 20% = -0.84
• 30% = -0.52
• 40% = -0.25
• 50% = 0
• 60% = 0,25
• 70% = 0,52
• 80% = 0,84
• 90% = 1,28
• 100% = 3,0

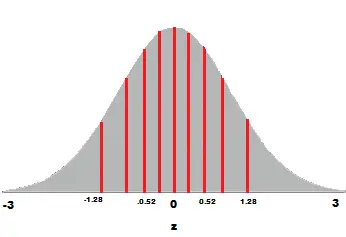
Algunos de los valores z representados en el gráfico.

Paso 4: Grafique los valores de su conjunto de datos (Paso 1) contra sus puntos de corte de distribución normal (Paso 3). Usé Open Office para este gráfico:

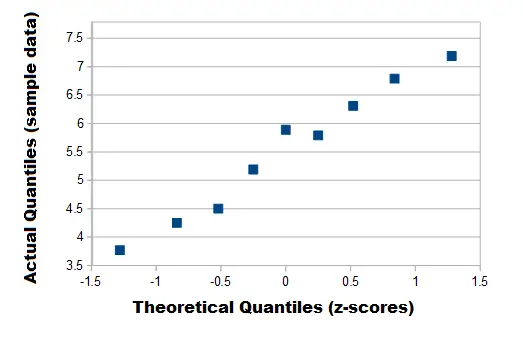
La línea (casi) recta en este gráfico qq indica que los datos son aproximadamente normales.

Nota : este ejemplo usó la distribución normal estándar , pero si cree que sus datos podrían provenir de una distribución normal diferente (es decir, una con una media y una desviación estándar diferentes), entonces podría usarla en su lugar.

Gráficas QQ y el supuesto de normalidad

El supuesto de normalidad es un supuesto importante para muchas pruebas estadísticas; asume que está tomando muestras de una población normalmente distribuida. El gráfico QQ normal es una forma de evaluar la normalidad. Sin embargo, no tiene que usar la distribución normal como comparación para sus datos; puede usar cualquier distribución continua como comparación (por ejemplo, una distribución de Weibull o una distribución uniforme ), siempre que pueda calcular los cuantiles. De hecho, un procedimiento común es probar varias distribuciones diferentes con la gráfica QQ para ver si alguna se ajusta bien a sus datos.

¡ Visite nuestro canal de YouTube para ver cientos de estadísticas elementales y videos de probabilidad!

Referencias

Agresti A. (1990) Análisis de datos categóricos. John Wiley and Sons, Nueva York.
Gonick, L. (1993). La guía de dibujos animados de estadísticas . Harper Perennial.
Vogt, WP (2005). Diccionario de estadística y metodología: una guía no técnica para las ciencias sociales . SABIO.
Wheelan, C. (2014). Estadísticas desnudas . WW Norton y compañía