Actualizado por ultima vez el 19 de diciembre de 2021, por Luis Benites.
¿Qué es el supuesto de normalidad?
La suposición de normalidad significa que debe asegurarse de que sus datos se ajusten aproximadamente a una forma de curva de campana antes de ejecutar ciertas pruebas estadísticas o regresión. Las pruebas que requieren datos normalmente distribuidos incluyen:
- Prueba t para muestras independientes.
- Modelado Lineal Jerárquico .
- ANCOVA .
- Prueba de bondad de ajuste .
Cómo probar la normalidad
Tiene dos formas principales de probar la normalidad: observar un gráfico o ejecutar una prueba que está diseñada específicamente para probar la normalidad. Los datos no tienen que ser perfectamente normales. Sin embargo, los datos que definitivamente no cumplen con la suposición de normalidad le darán resultados deficientes para ciertos tipos de pruebas (es decir, aquellas que establecen que se debe cumplir la suposición). ¿Qué tan cerca tienen sus datos de cumplir con la prueba de normalidad? Esta es una llamada de juicio.
Si no se siente cómodo haciendo ese juicio (que generalmente se basa en la experiencia con las estadísticas), entonces es mejor que realice una prueba estadística (desplácese hacia abajo para ver las opciones de prueba). Dicho esto, algunas de las pruebas pueden ser engorrosas de usar e implican encontrar estadísticas de prueba y valores críticos.
¿Atascado en qué opción elegir? Si eres nuevo en estadísticas, el gráfico más fácil de descifrar es el histograma. La prueba más fácil de ejecutar es probablemente la prueba de Jarque-Bera .
Uso de un gráfico para una prueba de normalidad.
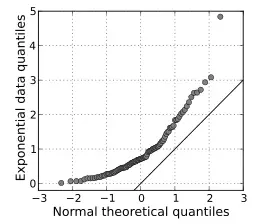
Gráfico AQQ que muestra la línea de referencia de 45 grados.
1. Gráfico QQ .
Un gráfico QQ compara dos distribuciones diferentes. Si los dos conjuntos de datos provienen de la misma distribución, los puntos caerán en una línea de referencia de 45 grados. Para usar este tipo de gráfico para la suposición de normalidad, compare sus datos con datos de una distribución con normalidad conocida .
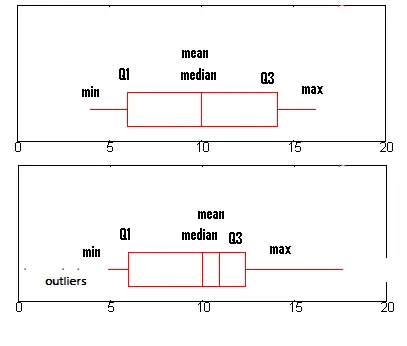
Diagramas de caja para datos distribuidos normalmente (arriba) y datos no normales (abajo).
2. Diagrama de caja .
Dibuja un diagrama de caja de tus datos. Si sus datos provienen de una distribución normal , la caja será simétrica con la media y la mediana en el centro. Si los datos cumplen con el supuesto de normalidad, también debería haber pocos valores atípicos .
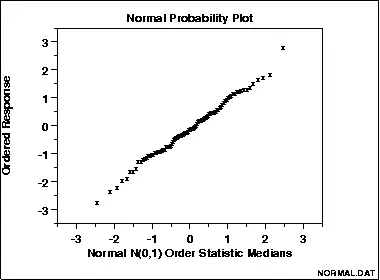
Una gráfica de probabilidad normal que muestra datos que son aproximadamente normales.
3. Gráfica de probabilidad normal.
La gráfica de probabilidad normal fue diseñada específicamente para probar el supuesto de normalidad. Si sus datos provienen de una distribución normal, los puntos en el gráfico formarán una línea.
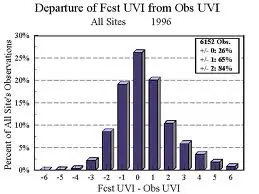
Datos normalmente distribuidos en una curva de campana clásica. Imagen: NASA
4. Histograma.
El popular histograma puede darle una buena idea sobre si sus datos cumplen con la suposición. Si sus datos se ven como una curva de campana: entonces probablemente sea normal.
Pruebas estadísticas de normalidad
Tienes muchas opciones para probar la normalidad. La mayoría de estos se incluyen con paquetes estadísticos como SPSS .
- Prueba de normalidad chi-cuadrado . Puede usar una prueba de chi cuadrado para la normalidad. La ventaja es que es relativamente fácil de usar, pero no es una prueba muy sólida. Si tiene una muestra pequeña (menos de 20), puede ser la única prueba que puede usar. Para muestras más grandes, es mucho mejor elegir otra opción.
- Test de D´Agostino-Pearson . Esto utiliza la asimetría y la curtosis para ver si sus datos coinciden con los datos normales. Requiere que el tamaño de su muestra sea superior a 20.
- Prueba de Jarque-Bera . Esta prueba común también es relativamente sencilla. Al igual que D’Agostino-Pearson, la idea básica es que prueba el sesgo y la curtosis de sus datos para ver si coinciden con lo que esperaría de una distribución normal. Cuanto más grande es la estadística JB, más se desvían los datos de lo normal.
- Prueba de bondad de ajuste de Kolmogorov-Smirnov . Esto compara sus datos con una distribución conocida (es decir, una distribución normal).
- Prueba de Lilliefors . La prueba de Lilliefors calcula una estadística de prueba T que se puede comparar con un valor crítico . Si la estadística de prueba es mayor que el valor crítico, es una señal de que sus datos no son normales. También calcula un valor p para su distribución, que compara con un nivel de significancia .
- Prueba de Shapiro-Wilk Esta prueba le dirá si una muestra aleatoria proviene de una distribución normal. La prueba te da un valor W; los valores pequeños indican que su muestra no se distribuye normalmente.
Referencias
Klein, G. (2013). La caricatura Introducción a la estadística. Colina y Wamg.
Kotz, S.; et al., editores. (2006), Enciclopedia de Ciencias Estadísticas , Wiley.
Vogt, WP (2005). Diccionario de estadística y metodología: una guía no técnica para las ciencias sociales . SABIO.
Wheelan, C. (2014). Estadísticas desnudas . WW Norton y compañía
