Contenido de este artículo
- 1 ¿Qué es el análisis de componentes principales?
- 2 Regresión de componentes principales (PCA)
- 3 PARAFAC
- 4 ¿Qué es el análisis de correspondencias?
- 5 Análisis de correspondencias múltiples
- 6 ¿Qué es el análisis de correlación canónica (CCA)?
- 7 Ejemplo de la vida real
- 8 ¿Qué es el análisis de redundancia?
- 9 Supuestos para el análisis de redundancia
- 10 Artículos relacionados
- 11 Referencias
- 12 Redactor del artículo
- 13 ¿Te hemos ayudado?
Actualizado el 3 de septiembre de 2021, por Luis Benites.
¿Qué es el análisis de componentes principales?
El Análisis de Componentes Principales (PCA) es una herramienta que tiene dos propósitos principales:
- Para encontrar la variabilidad en un conjunto de datos.
- Reducir las dimensiones del conjunto de datos.
Reducir dimensiones significa que se elimina la redundancia en los datos; Esto puede hacer que los patrones en el conjunto de datos sean más claros. Por lo tanto, el análisis de componentes principales es una buena herramienta para usar si sospecha que tiene redundancia en su conjunto de datos. La redundancia no significa que las variables sean idénticas; significa que existe una fuerte correlación entre ellos. Por ejemplo, supongamos que está realizando una encuesta de servicio al cliente con las siguientes cuatro preguntas en las que los clientes califican su satisfacción en una escala del 1 al 10:
- El tiempo de envío fue satisfactorio.
- Recibí mi artículo cuando esperaba recibirlo.
- El artículo era como se describe.
- El artículo se ajusta a la necesidad por la que lo compré.
Las preguntas 1 y 2 se refieren al tiempo, y las preguntas 3 y 4 se refieren al artículo real comprado. Si ejecutó el Análisis de componentes principales en este ejemplo simple, las cuatro variables separadas teóricamente podrían reducirse a dos (tiempo y costo). En la vida real, los conjuntos de datos pueden contener cientos o miles de variables, lo que hace imposible identificar la redundancia. Ahí es donde entra el Análisis de Componentes Principales; borra el » ruido » para permitirle identificar patrones en los datos.
El análisis de componentes principales reduce las dimensiones al proyectar todo el conjunto de datos en un espacio completamente separado. Las variables originales se transforman en un nuevo conjunto de variables artificiales, que son los «Componentes Principales» del Análisis de Componentes Principales. Estos componentes pueden ser extremadamente útiles como variables de criterio o variables predictoras en análisis de datos posteriores .
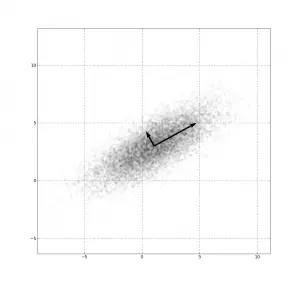
Imagen: Ben FrantzDale|Wikimedia Commons
Regresión de componentes principales (PCA)
La regresión de componentes principales se basa en el análisis de componentes principales. Se usa cuando su conjunto de datos exhibe multicolinealidad . Esto significa que aunque las estimaciones de mínimos cuadrados están sesgadas , las variaciones pueden estar demasiado lejos del valor real. PCA agrega cierto sesgo al modelo de regresión y reduce el error estándar . El primer paso en PCA es el mismo que en el Análisis de Componentes Principales: identificar los componentes principales. Luego se realiza una regresión sobre esos componentes.
PARAFAC
El análisis factorial paralelo (PARAFAC) es una generalización del análisis de componentes principales a matrices de orden superior. Es útil para el análisis exploratorio de datos en conjuntos de datos muy particulares, por ejemplo, si tiene datos de tres vías (es decir, puntuaciones de n personas en m variables medidas en p ocasiones 1 ). Donde PARAFAC difiere del Análisis de Componentes Principales es que PARAFACE produce componentes únicos.
¿Qué es el análisis de correspondencias?
El análisis de correspondencias (CA) es un caso especial de PCA. PCA explora relaciones entre variables en tablas con medición continua, mientras que el análisis de correspondencia se utiliza para tablas de contingencia . Las tablas de contingencia son una forma de representar conjuntos de datos que se dividen en dos o más categorías.

Una tabla de contingencia. Imagen: Departamento de Agricultura de Michigan
El análisis de correspondencias se puede utilizar para todo, desde simples tablas de doble entrada hasta tablas más complejas de varias entradas. CA es muy útil para situaciones más complejas, ya que simplifica los datos y proporciona una descripción detallada de casi toda la información obtenida de los datos. Su función principal es producir una pantalla gráfica que contenga «puntos» que representen filas y columnas. El objetivo es producir una vista general de los datos en un espacio de baja dimensión (es decir, un gráfico 2D) que sea fácil de interpretar.
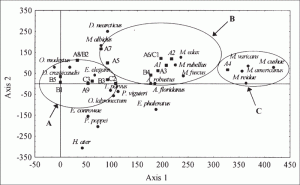
Ejemplo de un gráfico CA. Imagen: USGS.gov
Matemáticamente, el análisis de correspondencias es una forma de descomponer la estadística de chi-cuadrado en componentes debido a las filas y columnas de la tabla de contingencia. En términos más simples, es una forma de asignar orden a las categorías.
Análisis de correspondencias múltiples
El análisis de correspondencia múltiple es una extensión de CA para investigar las relaciones entre varias variables dependientes categóricas . Debe usarse cuando su conjunto de datos observados se describe mediante una serie de variables nominales con varios niveles. Cada nivel debe tener un código binario. Por ejemplo, si tiene un nivel de jubilado/no jubilado, jubilado podría ser «0» y no jubilado podría ser «1». Las entradas para MCA son a través de una tabla Burt .
Los nombres alternativos para esta técnica incluyen: escala dual, escala óptima y método de cuantificación. En términos técnicos, el Análisis de Correspondencias Múltiples se realiza utilizando CA en una matriz de indicadores (o matriz de diseño); Las filas son casos y las columnas son categorías de variables. Las dos diferencias principales en la salida son:
- Se debe modificar la interpretación de las diferencias entre puntos.
- Los porcentajes de las varianzas explicadas deben corregirse.
¿Qué es el análisis de correlación canónica (CCA)?
El análisis de correlación canónica es una forma de encontrar asociaciones entre dos conjuntos de datos. Al igual que el Coeficiente de Correlación , el CCA mide la relación entre variables . La diferencia del análisis de correlación canónica es que se usa específicamente para encontrar las relaciones entre dos conjuntos de variables .
Por ejemplo, un investigador educativo puede querer encontrar la asociación entre diferentes medidas de capacidad escolar y éxito en la escuela.
Es apropiado usar CCA en las mismas situaciones en las que podría usar el análisis de regresión múltiple , pero cuando tiene múltiples variables de resultado interrelacionadas . CCA no se recomienda para conjuntos de datos pequeños. Los métodos de análisis multivariante similares incluyen:
- Regresión múltiple multivariante, que es una alternativa si no está interesado en la dimensionalidad (las dimensiones canónicas son idénticas a los factores en el Análisis factorial ).
- Regresiones separadas de mínimos cuadrados ordinarios , una para cada variable en un conjunto. Sin embargo, esta opción no producirá resultados multivariados y tampoco le dará ninguna información sobre la dimensionalidad.
El propósito del análisis de correlación canónica es explicar la variabilidad dentro y entre conjuntos a través de la identificación de varios conjuntos de variables canónicas. Las variables canónicas son nuevas variables formadas al hacer una combinación lineal de dos o más variables de los conjuntos de datos. Al ejecutar CCA, elige ponderaciones que maximicen la correlación entre estos conjuntos de variables.
Las siguientes dos imágenes de variables canónicas se toman de un gráfico generado por SAS. Muestran dos pares de variables canónicas, graficados contra una línea de regresión para ver qué tan bien encajan los pares (fuente: PSU.edu).
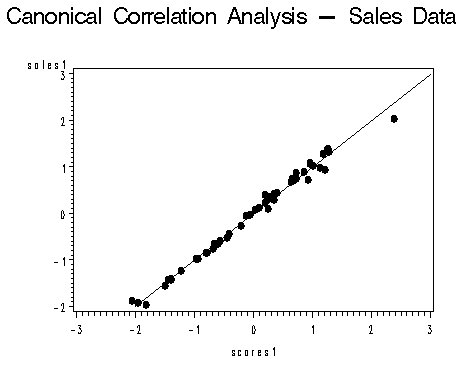
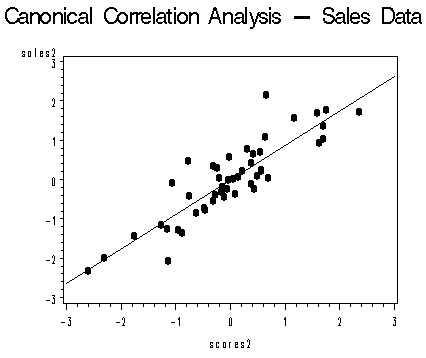
Ejemplo de la vida real
El análisis de correlación canónica se puede utilizar en experimentos para comparar dos conjuntos de variables y ver qué tienen en común. Por ejemplo, podría comparar dos pruebas de personalidad de psicología bien conocidas, el Inventario de personalidad multifásico de Minnesota (MMPI) y el Inventario de personalidad NEO revisado. Cuando compare los conjuntos con CCA, podrá ver cómo los factores del MMPI se relacionan con los factores de los NEO. Esto da como resultado que pueda ver qué tienen en común las pruebas y qué varianza se comparte entre las pruebas. Por ejemplo, puede encontrar que se comparte una buena cantidad de agresividad o introversión entre las pruebas.
¿Qué es el análisis de redundancia?
El análisis de redundancia es la versión restringida del análisis de componentes principales. Restringido básicamente significa reducción de dimensiones. Esta reducción es lo que conduce a resultados más comprensibles.
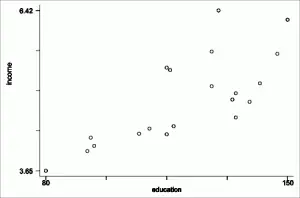
El análisis de redundancia es una extensión de la regresión lineal múltiple. Imagen: Universidad de Columbia
El análisis de redundancia es una forma de resumir relaciones lineales en un conjunto de variables dependientes que están influenciadas por un conjunto de variables independientes . Es una extensión de la regresión lineal múltiple . El método utiliza una combinación de regresión lineal y análisis de componentes principales (PCA).
- Primero se aplica la regresión lineal para representar Y como una función de X.
- A continuación, PCA se aplica a una matriz de los resultados para proporcionar una representación visual.
El análisis de redundancia es similar al análisis de correlación canónica. Tanto en CCA como en el análisis de redundancia, se maximiza la correlación de los componentes extraídos de las tablas. Sin embargo, se maximizan de formas ligeramente diferentes:
- En el análisis de correlación canónica, los componentes se extraen de ambas tablas para maximizar las correlaciones.
- En el análisis de redundancia, los componentes de X se extraen de las tablas para que tengan una correlación máxima con Y. Luego, los componentes de Y se extraen para que tengan una correlación máxima con X.
Supuestos para el análisis de redundancia
Dado que el análisis de redundancia es una extensión de la regresión lineal , se aplican las mismas suposiciones. Por ejemplo, antes de realizar un análisis de redundancia a un conjunto de datos, debe verificar la dependencia lineal. Por ejemplo:
- El aumento de los valores de X debería resultar en un aumento de los valores de Y.
- Si las variables X se duplican, los valores Y también deberían duplicarse.
Además, la cantidad de variables explicativas ( variables independientes ) debe ser menor que la cantidad de objetos en su matriz de datos. Sus variables independientes y variables dependientes también deben tener las mismas unidades físicas. Si no lo hacen, debe estandarizarlos (es decir, encontrar sus puntuaciones z ) antes de ejecutar el análisis de redundancia. Una excepción son los datos de conteo sin procesar, que no deben estandarizarse.
Artículos relacionados
Referencias
Imagen de PSU.edu recuperada el 14 de diciembre de 2020 de: https://onlinecourses.science.psu.edu/stat505/node/69
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo:

MUY BIEN, LE FELICITO, ME GUSTARÍA CONVERSAR CON USTED, DE SER POSIBLE. TAMBIÉN TRABAJO EN EL ÁREA DEL SABER DE LA ESTADÍSTICA. SI ME PERMITE LE PUEDO ENVIAR UN RESUMEN DE MI HOJA DE VIDA. MI CORREO ES gomezdegraves@gmail.com
MUCHAS GRACIAS
Buenos días, le envié un correo.