Contenido de este artículo
- 0
- 0
- 0
- 0
Actualizado el 7 de junio de 2022, por Luis Benites.
¿Qué es la multicolinealidad?
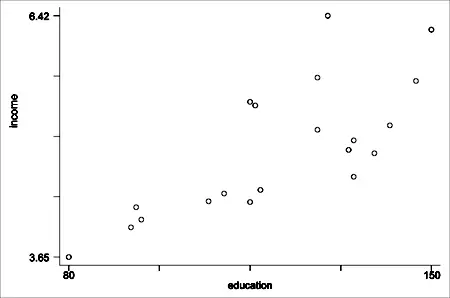
La multicolinealidad puede afectar negativamente los resultados de su regresión.
La multicolinealidad generalmente ocurre cuando hay altas correlaciones entre dos o más variables predictoras . En otras palabras, una variable predictora se puede utilizar para predecir la otra. Esto crea información redundante, sesgando los resultados en un modelo de regresión. Ejemplos de variables predictoras correlacionadas (también denominadas predictores multicolineales) son: la altura y el peso de una persona, la edad y el precio de venta de un automóvil, o los años de educación y los ingresos anuales.
Una forma fácil de detectar la multicolinealidad es calcular los coeficientes de correlación para todos los pares de variables predictoras. Si el coeficiente de correlación, r, es exactamente +1 o -1, esto se denomina multicolinealidad perfecta. Si r está cerca o exactamente -1 o +1, una de las variables debe eliminarse del modelo si es posible.
Es más común que la multicolinealidad muestre su fea cabeza en los estudios observacionales; es menos común con los datos experimentales. Cuando la condición está presente, puede resultar en estimaciones de regresión inestables y poco confiables. Varios otros problemas pueden interferir con el análisis de los resultados, incluyendo:
- La estadística t generalmente será muy pequeña y los intervalos de confianza de los coeficientes serán muy amplios. Esto significa que es más difícil rechazar la hipótesis nula .
- El coeficiente de regresión parcial puede ser una estimación imprecisa; los errores estándar pueden ser muy grandes.
- Los coeficientes de regresión parcial pueden tener cambios de signo y/o magnitud a medida que pasan de una muestra a otra.
- La multicolinealidad dificulta medir el efecto de las variables independientes sobre las variables dependientes .
¿Qué causa la multicolinealidad?
Los dos tipos son:
- Multicolinealidad basada en datos: causada por experimentos mal diseñados, datos que son 100% observacionales o métodos de recopilación de datos que no se pueden manipular. En algunos casos, las variables pueden estar altamente correlacionadas (generalmente debido a la recopilación de datos de estudios puramente observacionales) y no hay error por parte del investigador. Por esta razón, debe realizar experimentos siempre que sea posible, estableciendo el nivel de las variables predictoras de antemano.
- Multicolinealidad estructural : causada por usted, el investigador, creando nuevas variables predictoras.
Las causas de la multicolinealidad también pueden incluir:
- Datos insuficientes . En algunos casos, recopilar más datos puede resolver el problema.
- Las variables ficticias pueden usarse incorrectamente. Por ejemplo, el investigador puede no excluir una categoría o agregar una variable ficticia para cada categoría (por ejemplo, primavera, verano, otoño, invierno).
- Incluir una variable en la regresión que en realidad es una combinación de otras dos variables . Por ejemplo, incluir el «ingreso total de inversiones» cuando el ingreso total de inversiones = ingresos de acciones y bonos + ingresos de intereses de ahorros.
- Incluyendo dos variables idénticas (o casi idénticas) . Por ejemplo, peso en libras y peso en kilos, o ingresos de inversiones e ingresos de ahorros/bonos.
Siguiente : Factores de Inflación de Varianza .
Referencias
Beyer, WH CRC Standard Mathematical Tables, 31ª ed. Boca Raton, FL: CRC Press, págs. 536 y 571, 2002.
Dodge, Y. (2008). La Enciclopedia Concisa de Estadística . Saltador.
Klein, G. (2013). La caricatura Introducción a la estadística. Colina y Wamg.
Vogt, WP (2005). Diccionario de estadística y metodología: una guía no técnica para las ciencias sociales . SABIO.
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo:
