Contenido de este artículo
- 0
- 0
- 0
- 0
Actualizado el 7 de junio de 2022, por Luis Benites.
El alfa de Krippendorff (también llamado coeficiente de Krippendorff ) es una alternativa al Kappa de Cohen para determinar la confiabilidad entre evaluadores .
Alfa de Krippendorff:
- Ignora por completo los datos que faltan.
- Puede manejar varios tamaños de muestra, categorías y números de evaluadores.
- Se aplica a cualquier nivel de medición (es decir, ( nominal, ordinal, de intervalo, de razón ).
Comúnmente utilizado en el análisis de contenido para cuantificar el grado de acuerdo entre evaluadores, difiere de la mayoría de las otras medidas de confiabilidad entre evaluadores porque calcula el desacuerdo (en oposición al acuerdo). Esta es una de las razones por las que la estadística es posiblemente más confiable, pero algunos investigadores informan que, en la práctica, los resultados de alfa y kappa son similares (Dooley).
Cálculo del Alfa de Krippendorff
La fórmula básica para alfa es una proporción (desacuerdo observado/desacuerdo esperado). La relación es engañosamente simple, porque el método en realidad es computacionalmente complejo e involucra métodos de remuestreo como bootstrap . Esta es una gran desventaja (Osborne). Puede obtener una idea de los cálculos involucrados a partir de la siguiente fórmula.
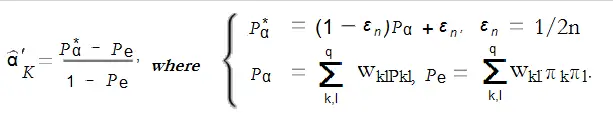
Puede encontrar un buen ejemplo de cuán complejo puede llegar a ser el cálculo en el artículo de Krippendorf de 2011, Computing Krippendorff’s Alpha-Reliability ( pdf descargable ). La entrada de Wikipedia también tiene un ejemplo (algo esotérico), donde se describe la construcción de una matriz de coincidencia para una matriz de 3 evaluadores y 15 elementos.
Se han creado muchas macros para calcular el alfa, lo que abre el uso del alfa de Krippendorff a un público más amplio. Éstos incluyen:
- MATLAB : existen varias macros, incluidas la de Jana Eggink ( descargable aquí ) y la de Jeffrey Girard ( descargable aquí ).
¿Qué significan los resultados?
Los valores van de 0 a 1, donde 0 es perfecto desacuerdo y 1 es perfecto acuerdo. Krippendorff sugiere: “[E]s costumbre exigir α ≥ .800. Donde las conclusiones tentativas aún son aceptables, α ≥ .667 es el límite más bajo concebible (2004, p. 241).”
Referencias:
Dooley, K. (2017). Lenguaje de programación de cuestionarios. Informe de confiabilidad entre evaluadores. Recuperado el 5 de julio de 2017 de: http://qpl.gao.gov/ca050404.htm.
Hayes, AF Mis macros y código para SPSS y SAS. Recuperado el 6 de julio de 2017 de: http://afhayes.com/spss-sas-and-mplus-macros-and-code.html
Hayes, AF & Krippendorff, K. (2007). Respondiendo a la demanda de una medida de fiabilidad estándar para la codificación de
datos. Métodos y medidas de comunicación 1,1:77-89.
Jason Osborn. Mejores Prácticas en Métodos Cuantitativos .
Krippendorff, K. (2004). Análisis de contenido: Una introducción a su metodología. Thousand Oaks, California: Sabio.
Krippendorff, K. (2011). «Cálculo de la confiabilidad alfa de Krippendorff». Filadelfia: Annenberg School for Communication Department Papers. Recuperado el 6 de julio de 2011 de: http://repository.upenn.edu/cgi/viewcontent.cgi?article=1043&context=asc_papers
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo:
