Actualizado por ultima vez el 4 de junio de 2022, por Luis Benites.
¿Qué es la confiabilidad entre evaluadores?
La confiabilidad entre evaluadores es el nivel de acuerdo entre evaluadores o jueces . Si todos están de acuerdo, la TIR es 1 (o 100 %) y si todos están en desacuerdo, la TIR es 0 (0 %). Existen varios métodos para calcular la TIR, desde los más simples (p. ej., porcentaje de concordancia) hasta los más complejos (p. ej . , Kappa de Cohen ). El que elija depende en gran medida del tipo de datos que tenga y de cuántos evaluadores haya en su modelo.
Métodos de confiabilidad entre evaluadores
1. Acuerdo porcentual para dos evaluadores
La medida básica para la confiabilidad entre evaluadores es un acuerdo porcentual entre evaluadores .
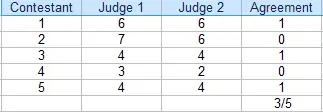
En esta competencia, los jueces acordaron 3 de 5 puntajes. El porcentaje de concordancia es 3/5 = 60%.
Para encontrar el porcentaje de acuerdo para dos evaluadores , una tabla (como la de arriba) es útil.
- Cuente el número de calificaciones de acuerdo. En la tabla anterior, eso es 3.
- Cuente el número total de calificaciones. Para este ejemplo, eso es 5.
- Divide el total por el número de acuerdo para obtener una fracción: 3/5.
- Convertir a porcentaje: 3/5 = 60%.
El campo en el que esté trabajando determinará el nivel de acuerdo aceptable. Si se trata de una competencia deportiva, puede aceptar un acuerdo de calificación del 60 % para decidir un ganador. Sin embargo, si busca datos de especialistas en cáncer que deciden un curso de tratamiento, querrá un acuerdo mucho más alto, superior al 90 %. En general, por encima del 75 % se considera aceptable para la mayoría de los campos.
Acuerdo porcentual para evaluadores múltiples
Si tiene varios evaluadores, calcule el porcentaje de acuerdo de la siguiente manera:
Paso 1: Haz una tabla de tus calificaciones. Para este ejemplo, hay tres jueces:
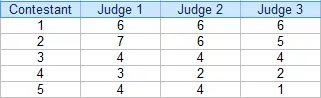
Paso 2: agregue columnas adicionales para las combinaciones (pares) de jueces. Para este ejemplo, los tres pares posibles son: J1/J2, J1/J3 y J2/J3.
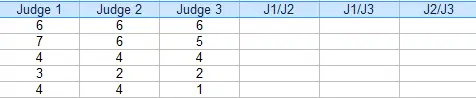
Paso 3: Para cada par, ponga un «1» para acuerdo y «0» para acuerdo. Por ejemplo, el concursante 4, el juez 1/juez 2 no estuvo de acuerdo (0), el juez 1/juez 3 no estuvo de acuerdo (0) y el juez 2/juez 3 estuvo de acuerdo (1).

Paso 4: sume los 1 y los 0 en una columna de acuerdo:

Paso 5: encuentre la media de las fracciones en la columna de concordancia.
Media = (3/3 + 0/3 + 3/3 + 1/3 + 1/3) / 5 = 0,53 o 53 %.
La confiabilidad entre evaluadores para este ejemplo es del 54%.
Desventajas
Como probablemente se dará cuenta, calcular los acuerdos porcentuales para más de un puñado de evaluadores puede volverse engorroso rápidamente. Por ejemplo, si tuviera 6 jueces, tendría que calcular 16 combinaciones de pares para cada concursante (use nuestra calculadora de combinaciones para averiguar cuántos pares obtendría para varios jueces).
Una falla importante con este tipo de confiabilidad entre evaluadores es que no tiene en cuenta el acuerdo aleatorio y sobreestima el nivel de acuerdo. Esta es la razón principal por la cual el porcentaje de concordancia no debe usarse para trabajos académicos (es decir, disertaciones o publicaciones académicas).
Metodos alternativos
Se han desarrollado varios métodos que son más fáciles de calcular (por lo general, están integrados en paquetes de software estadístico) y tienen en cuenta el azar:
- Si tiene uno o dos pares significativos, use la correlación entre clases (equivalente al coeficiente de correlación de Pearson ).
- Si tiene más de un par de pares, use la correlación intraclase . Este es uno de los métodos de TIR más populares y se usa para dos o más evaluadores.
- Kappa de Cohen : comúnmente utilizado para variables categóricas.
- Kappa de Fleiss: similar al Kappa de Cohen, adecuado cuando tiene un número constante de m evaluadores muestreados aleatoriamente de una población de evaluadores, con una muestra diferente de m codificadores calificando cada sujeto.
- El coeficiente AC2 de Gwet se calcula fácilmente en Excel con el complemento AgreeStat.com .
- Se puede decir que el Alpha de Krippendorff es la mejor medida de la confiabilidad entre evaluadores, pero es computacionalmente complejo.
Referencias
Beyer, WH CRC Standard Mathematical Tables, 31ª ed. Boca Raton, FL: CRC Press, págs. 536 y 571, 2002.
Everitt, BS; Skrondal, A. (2010), The Cambridge Dictionary of Statistics , Cambridge University Press.
Klein, G. (2013). La caricatura Introducción a la estadística. Colina y Wamg.
Vogt, WP (2005). Diccionario de estadística y metodología: una guía no técnica para las ciencias sociales . SABIO.

