Contenido de este artículo
- 0
- 0
- 0
- 0
Actualizado el 19 de julio de 2024, por Luis Benites.
Resumen
La variabilidad es una medida de cuán dispersos o diferentes son los valores en un conjunto de datos. En otras palabras, indica el grado en que los datos varían entre sí. La variabilidad puede ser representada de varias maneras, como el rango, la varianza, la desviación estándar, y el rango intercuartílico. Una alta variabilidad significa que los datos están ampliamente dispersos, mientras que una baja variabilidad indica que los datos están agrupados cerca de la media.
¿Qué es la Variabilidad en Estadística?
La variabilidad (también llamada propagación o dispersión) se refiere a qué tan disperso está un conjunto de datos. La variabilidad le brinda una manera de describir cuánto varían los conjuntos de datos y le permite usar estadísticas para comparar sus datos con otros conjuntos de datos. Las cuatro formas principales de describir la variabilidad en un conjunto de datos son:
Distancia
El rango es la cantidad entre el artículo más pequeño y el más grande del conjunto. Puedes encontrar el rango restando el número más pequeño del más grande. Por ejemplo, digamos que ganó $250 una semana, $30 la semana siguiente y $800 la tercera semana. El rango de su pago (es decir, cuánto varía) es de $30 a $800.
Rango intercuartil
El rango intercuartílico es casi lo mismo que el rango, solo que en lugar de indicar el rango para todo el conjunto de datos, está dando la cantidad para los » cincuenta del medio «. A veces es más útil que el rango porque le dice dónde se encuentran la mayoría de sus valores. La fórmula es IQR = Q3 – Q1, donde Q3 es el tercer cuartil y Q1 es el primer cuartil. Básicamente, toma uno de los valores más pequeños (en el percentil 25) y lo resta de uno de los valores más grandes (en el percentil 75). La siguiente gráfica de caja muestra el rango intercuartílico, representado por la caja. Los bigotes (las líneas que salen de cada lado de la caja) representan el primer cuarto de los datos y el último cuarto.
Más información: Rango intercuantilico
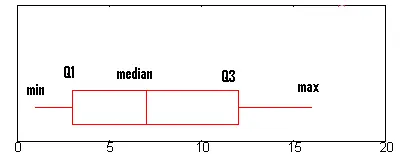
Diferencia
La varianza de un conjunto de datos le da una idea aproximada de cuán dispersos están sus datos. Un número pequeño para la varianza significa que su conjunto de datos está muy agrupado y un número grande significa que los valores están más dispersos. La varianza rara vez es útil excepto para calcular la desviación estándar.
Desviación Estándar
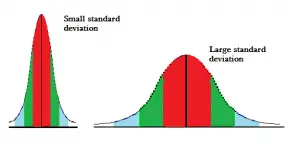
La desviación estándar le indica qué tan estrechamente se agrupan sus datos alrededor de la media (el promedio ). Una SD pequeña indica que sus datos están muy agrupados; también tendrá una curva de campana más alta ; una SD grande le dice que sus datos están más dispersos.
Más ejemplos de Variabilidad
Ejemplo 1: Variabilidad Baja
Considera dos conjuntos de datos:
| Conjunto A | Conjunto B |
|---|---|
| 5 | 5 |
| 6 | 5 |
| 5 | 5 |
| 6 | 5 |
| 5 | 5 |
En este ejemplo, el Conjunto A tiene una baja variabilidad porque los valores están muy cerca entre sí. Los valores fluctúan entre 5 y 6, lo que indica poca dispersión.
Ejemplo 2: Variabilidad Alta
Ahora, considera estos dos conjuntos de datos:
| Conjunto C | Conjunto D |
|---|---|
| 1 | 10 |
| 10 | 20 |
| 15 | 30 |
| 20 | 40 |
| 25 | 50 |
En este ejemplo, el Conjunto D tiene una alta variabilidad porque los valores están muy dispersos. Los valores varían ampliamente de 10 a 50, lo que indica una mayor dispersión.
Referencias
Everitt, BS; Skrondal, A. (2010), The Cambridge Dictionary of Statistics , Cambridge University Press.
Gonick, L. (1993). La guía de dibujos animados de estadísticas . Harper Perennial.
Redactor del artículo
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo:
