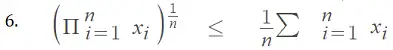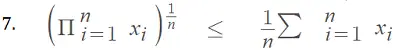Contenido de este artículo
- 0
- 0
- 0
- 0
Actualizado el 23 de marzo de 2022, por Luis Benites.
¿Qué es la media aritmética?
La media aritmética es otro nombre para la media o el promedio. Cuando alguien habla de la media de un conjunto de datos, por lo general se refiere a la media aritmética (la mayoría de la gente simplemente deja caer la palabra «aritmética»). Se llama con un nombre diferente para diferenciarlo de otros medios que se encuentran en las matemáticas, incluida la media geométrica .
La media está influenciada por los valores atípicos , por lo que no siempre es un buen indicador de dónde se encuentra el centro de un conjunto de datos. Para conjuntos de datos que tienen muchos valores bajos o muchos valores altos, la mediana suele ser una mejor manera de describir el «medio».
Cómo encontrar la media aritmética
Media aritmética Paso 1: suma los números
Encontrar la media aritmética requiere dos pasos: sume todos los números y luego divida por la cantidad de elementos en su conjunto. La media aritmética se encuentra exactamente de la misma manera que la media de una muestra («muestra» aquí solo significa una cantidad de elementos en su conjunto de datos). Mire el video o lea los pasos a continuación:
Cómo encontrar la media de una muestra Mira este video en YouTube .
Problema de ejemplo: encuentre la media aritmética de la velocidad promedio de conducción de un automóvil durante un viaje de 6 horas: 54 mph, 57 mph, 58 mph, 66 mph, 69 mph, 71 mph
Paso 1: suma todos los números: 54 + 57 + 58 + 66 + 69 + 71 = 375.
Paso 2: divide por el número de elementos del conjunto. Para este conjunto hay 6 números, entonces:
375/6 = 62,5.
Solución : la velocidad promedio de conducción es de 62,5 mph.
Para otro ejemplo con pasos, vea el siguiente artículo:
Cómo encontrar la media
Población frente a media muestral
Si sus datos son una población , entonces la media se llama media poblacional , representada por la letra μ. Si la lista es una muestra , se llama media muestral x̄.
Mostrar que la media aritmética es mayor que la media geométrica
La desigualdad de Jensen , que generalmente se enseña en un curso de estadística basado en cálculo , se puede usar para mostrar que la media aritmética de n escalares positivos x 1 ,x 2 ,…x n , es mayor o igual que su media geométrica , que es igual a Donde Π es la notación del producto .
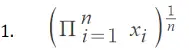
Esta afirmación se puede demostrar considerando una función convexa f(x) = -log x. Sea X una variable aleatoria discreta con valores x 1 ,x 2 ,…x n , y probabilidades 1/n [1]:
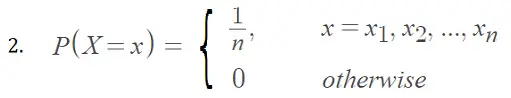
Por la desigualdad de Jensen:
E (-log X ) ≥ – log E( X ).
Sin embargo: y
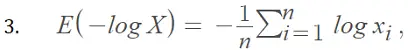
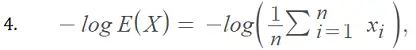
Con 3. y 4. en la desigualdad de Jensen, tenemos: o La función logaritmo es monótona creciente , por lo que podemos concluir que:
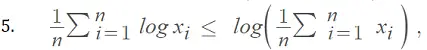
Visite nuestro canal de YouTube para ver cientos de videos de estadísticas y cálculos.
Referencias
[1] Khuri, A. Cálculo avanzado con aplicaciones en estadística. Segunda edicion. Wiley.¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo: