Actualizado por ultima vez el 3 de septiembre de 2021, por Luis Benites.
Es posible que desee leer primero las Partes 1 y 2 de Introducción a la estadística .
Cuando realizamos una encuesta o un experimento, a veces queremos encontrar un intervalo en el que podamos esperar encontrar la mayoría (95%) de los resultados; el intervalo que contiene el 95 % de los resultados se denomina intervalo de confianza del 95 % .
Mire el video para ver una introducción al intervalo de confianza del 95 por ciento:
Intervalos de confianza del 95 por ciento (Parte 3 de Introducción a las estadísticas) Mira este video en YouTube .
¿No puedes ver el vídeo? Haga clic aquí
Intervalo de confianza del 95 por ciento: un ejemplo de encuesta
Supongamos que un grupo de encuestadores desea determinar cuál podría ser el valor del parámetro de población , en función de una estadística muestral . Por ejemplo, un encuestador que obtenga un valor estadístico muestral del 34 % querrá calcular un intervalo de confianza del 95 % que rodee al 34 % y explicar qué podría decirnos ese intervalo sobre las opiniones de la población en general.
Vamos a explorar las sutilezas involucradas enviando 1,000 encuestadores para encuestar a la misma población y ver qué se les ocurre y cómo deben interpretar lo que se les ocurre. Pero primero necesitaremos preparar el escenario inventando una población que tenga ciertas características que conocemos, pero que ninguno de los encuestadores conoce. Nuestra comunidad inventada, Artesian Wells, tiene unos 70.000 habitantes. Se está debatiendo una nueva política de salud pública y, como somos omniscientes (todo lo sabemos), sabemos que el 40% de los residentes está de acuerdo con la nueva política. Solo nosotros sabemos esto. Queremos saber qué esperar cuando muchos, muchos encuestadores toman muestras aleatorias de 1000 personas de esta población. A los encuestados se les preguntará si están “de acuerdo” o “en desacuerdo” con algo, un binomio respuesta. Usaremos proporciones en lugar de porcentajes, con las proporciones redondeadas a dos decimales.
La figura 3.3 nos muestra la distribución muestral de qué esperar. (No se confunda: hay 1000 muestras aleatorias, y cada muestra tiene un tamaño de muestra de 1000). Según la inspección visual, observe que la gran mayoría de las proporciones de la muestra están en el intervalo de 0,37 a 0,43. Aproximadamente 950 de las 1000 proporciones de muestra están contenidas dentro del intervalo de 0,37 a 0,43, lo que indica que 0,37 a 0,43 es el intervalo de confianza del 95 por ciento que rodea la proporción de población de 0,40. La fórmula nos dará las mismas líneas límite. (Siéntase libre de verificar dos veces).
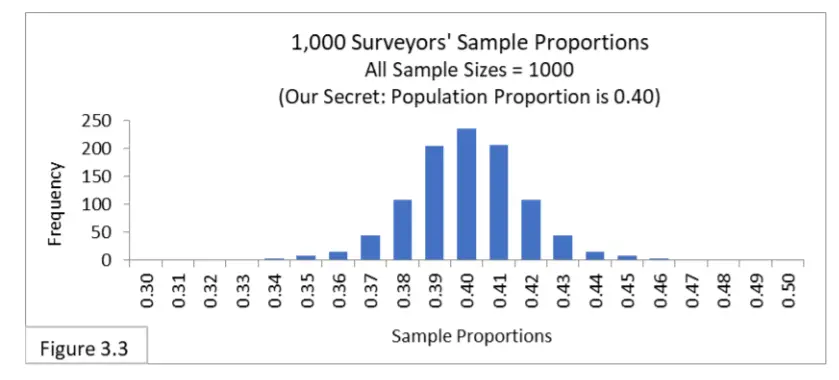
Siempre esperamos que el intervalo del 95% alrededor de la proporción de la población contenga el 95% de todas las proporciones muestrales obtenidas por muestreo aleatorio.
Ahora, contratamos 1,000 encuestadores independientes que se reúnen en la ciudad para hacer la encuesta de «acuerdo» o «desacuerdo». Los 1000 encuestadores obtienen su propia muestra aleatoria de 1000 residentes y calculan su propia estadística de acuerdo de proporción muestral. ¿Cómo analiza cada uno de los encuestadores individuales su proporción de muestra?
Fórmula del intervalo de confianza del 95 por ciento para proporciones de muestra
Veamos la fórmula para calcular los intervalos de confianza del 95 % para las proporciones de la muestra. Se parece mucho a la fórmula de la sección anterior. La variable p con un sombrero denota la proporción de la muestra (en oposición a la proporción de la población ). El término raíz cuadrada calcula el error estándar para la proporción de la muestra. El tamaño de la muestra está nuevamente representado por n. En cuanto a la constante 1,96, a veces redondeo 1,95996… errores estándar a 2 errores estándar para facilitar el cálculo; aquí, estoy siendo más preciso usando 1.96 errores estándar, que es más común.
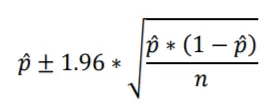
Cada uno de los 1000 encuestadores calcula su intervalo individual utilizando su valor de proporción muestral, y esperamos que el 95 % de los intervalos de confianza del 95 % de los encuestadores contengan la proporción de la población (0,4 en este ejemplo). Es posible que desee volver a leer esa oración varias veces, teniendo en cuenta que aunque nosotros, como sabelotodos, sabemos que la proporción de la población es 0,4, ninguno de los encuestadores tiene idea de qué es.
Es en este contexto que surgió el término «confianza» en «intervalo de confianza» : estamos seguros de que el 95 % de todos los intervalos de confianza del 95 % para los valores estadísticos de la muestra obtenidos mediante muestreo aleatorio contendrán el valor estadístico de la población. (¡Pero ningún encuestador individual sabrá si su intervalo de confianza contiene el valor del parámetro de población o no!)
En una palabra:
- Los 1000 encuestadores calculan sus intervalos de confianza individuales del 95%.
- Alrededor de 950 de ellos tendrán un intervalo que contenga la proporción de población.
- Alrededor de 50 de ellos no lo harán.
¿Qué nos dice el intervalo de confianza del 95 por ciento?
Veamos los intervalos de confianza del 95 % construidos a través de la fórmula por dos encuestadores: el primero obtuvo una proporción muestral de 0,38 y el segundo obtuvo una proporción muestral de 0,34.
Resultado del Topógrafo #1.
Utilizando la fórmula con una proporción de muestra de 0,38 y un tamaño de muestra de 1000, el intervalo de confianza del 95 por ciento es de 0,35 a 0,41 (redondeado).
Solo nosotros, que somos sabelotodos, sabemos que este intervalo de confianza del 95 por ciento contiene la proporción de población de 0,4
Resultado del topógrafo n.º 2.
Utilizando la fórmula con una proporción de muestra de 0,34 y un tamaño de muestra de 1000, el intervalo de confianza del 95 por ciento es de 0,31 a 0,37. Solo nosotros, que somos sabelotodos, sabemos que este intervalo de confianza del 95 por ciento no contiene la proporción poblacional de 0,4. Solo nosotros sabemos que este encuestador es uno del 5% de encuestadores desafortunados que por casualidad obtuvieron una muestra aleatoria engañosa. Esto se llama un error de tipo I.
En resumen,
- Esperamos que el intervalo de confianza del 95 por ciento alrededor de la proporción de la población contenga el 95 por ciento de todas las proporciones muestrales obtenidas por muestreo aleatorio. Hemos estado viendo esto todo el tiempo.
- Esperamos que el 95% de todos los intervalos de confianza del 95% basados en proporciones de muestras aleatorias contengan la proporción de la población. Vemos esto por primera vez aquí; más detalles se dan a continuación.
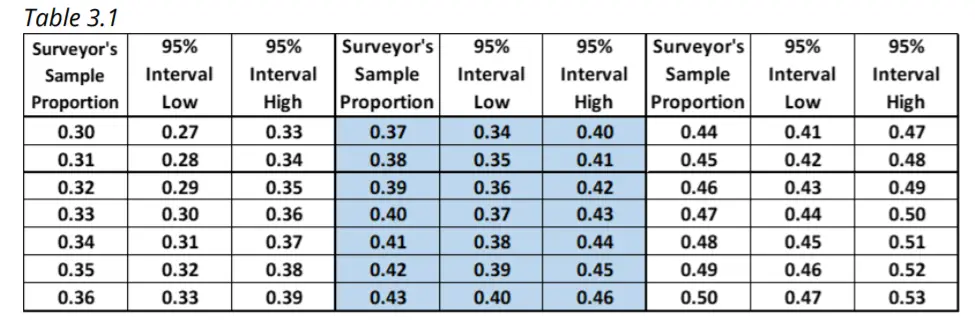
La Tabla 3.1 se divide en tres secciones, de izquierda a derecha, y muestra lo que obtendrán los distintos encuestadores. En general, la tabla muestra los intervalos de confianza para encuestadores con proporciones de muestra de 0,3 a 0,5; las proporciones muestrales 0,30 a 0,36 están en la sección izquierda, 0,37 a 0,43 están en la sección central (sombreada) y 0,44 a 0,50 están en la sección derecha. Observe que los 950 encuestadores esperados en la sección central (sombreada) con proporciones de muestra dentro del intervalo de 0,37 a 0,43 también tienen intervalos de confianza del 95 % que contienen la proporción de población de 0,40. Los 50 encuestadores esperados con proporciones muestrales fuera del intervalo de 0,37 a 0,43 (las secciones izquierda y derecha de la tabla) no tienen intervalos de confianza del 95 % que contengan la proporción poblacional de 0,40.
 Nuevamente, en resumen, y para enfatizar:
Nuevamente, en resumen, y para enfatizar:
- Esperamos que el intervalo de confianza del 95 % alrededor de la proporción de la población contenga el 95 % de todas las proporciones muestrales obtenidas por muestreo aleatorio.
- Esperamos que el 95% de todos los intervalos de confianza del 95% basados en proporciones de muestras aleatorias contengan la proporción de la población.
Debido a estos dos hechos, llegaremos a la misma conclusión ya sea que
- verificar si una proporción de muestra está fuera del intervalo del 95% que rodea una proporción de población hipotética, o
- compruebe si la proporción de la población hipotética está fuera del intervalo del 95% que rodea una proporción de muestra.
El análisis se puede hacer de cualquier manera.
He aquí una analogía rápida: Supongamos que una planta de estampado que fabrica monedas no funciona correctamente y produce monedas desequilibradas (es decir, injustas). Sin que nadie lo supiera, estas monedas injustas favorecían las cruces, y la probabilidad de que salga cara es de solo 0,4. Ahora digamos que 1000 personas lanzan estas monedas 1000 veces cada una, mientras cuentan y luego determinan la proporción de caras. ¿Cómo serían los resultados de las 1.000 personas? ¿Cómo sería un análisis de una sola moneda y sus 1000 lanzamientos? Respuesta: Al igual que el ejemplo de la encuesta anterior. Simplemente reemplace las palabras «de acuerdo» y «en desacuerdo» con «cara» y «cruz». Esperamos que el 95 % de los que lanzan monedas obtengan intervalos de confianza del 95 % que contienen 0,4, y el 5 % de los que lanzan monedas obtienen intervalos de confianza del 95 % que no contienen 0,4. En otras palabras, esperamos que el 95 % de los resultados sean verídicos y el 5 % engañosos. Pero nadie sabe si sus resultados son verídicos o engañosos. La razón por la que uso la palabra «verídico» es porque es la palabra perfecta: «Coincidiendo con la realidad». Lo estoy usando para significar lo contrario de engañoso.
Siguiente: Errores de tipo I y tipo II
Referencias
JE Kotteman. Análisis Estadístico Ilustrado – Fundamentos . Publicado vía Copyleft . Usted es libre de copiar y distribuir este contenido.
Kenney, JF y Keeping, ES «Límites de confianza para el parámetro binomial» y «Gráficos de intervalos de confianza». §11.4 y 11.5 en Matemáticas de Estadística, Pt. 1 , 3ª ed. Princeton, Nueva Jersey: Van Nostrand, págs. 167-169, 1962.

