Actualizado por ultima vez el 22 de agosto de 2021, por Luis Benites.
Anterior : supuestos estadísticos
Analizar la diferencia entre dos grupos usando proporciones binomiales
Hasta ahora, en Introducción a la estadística , hemos cubierto muchos fundamentos esenciales. Pongámoslos en acción mientras observamos otro tipo común de análisis que involucra proporciones binomiales. Estamos encuestando a la población de Flowing Wells, pero los compararemos con la población de un pueblo vecino, Artesian Wells. El motivo de nuestras encuestas es evaluar cómo se sienten los residentes acerca de una iniciativa del gobierno estatal recientemente propuesta.
El gobierno estatal está considerando aumentar los impuestos estatales para financiar algunos programas gubernamentales nuevos. Vamos a encuestar a los residentes de Flowing Wells como lo hemos estado haciendo, pero también vamos a encuestar a los residentes del pueblo cercano de Artesian Wells. Históricamente, se sabe que la ciudad de Flowing Wells se inclina hacia el socialismo y probablemente esté a favor de los nuevos impuestos y programas, pero se cree que la ciudad de Artesian Wells tiene una tendencia libertaria y probablemente no. La encuesta se realizará en cada uno de los dos pueblos para ver si las proporciones de residentes que están a favor de los nuevos impuestos y programas son diferentes en los dos pueblos.
La hipótesis nula correspondiente es que no son diferentes: no hay diferencia entre las proporciones de población de las comunidades de Flowing Wells y Artesian Wells . Es decir, la diferencia entre las proporciones de población de Flowing Wells y Artesian Wells es igual a cero.
La estadística muestral relevante es la proporción muestral de Flowing Wells menos la proporción muestral de Artesian Wells. (Usar la proporción de muestra de los pozos artesianos menos la proporción de muestra de los pozos que fluyen nos dará fundamentalmente los mismos resultados).
Desafortunadamente, la organización sin fines de lucro que realiza la encuesta solo tiene recursos para encuestar a 100 residentes al azar en cada ciudad. Primero, obtengamos una “vista de pájaro” de la situación. La hipótesis nula es que no hay diferencia entre las proporciones de población de las comunidades de Flowing Wells y Artesian Wells, así que veamos los resultados de la simulación que asumen que eso es cierto.
Proporciones Binomiales: Resultados de la Simulación
Supondremos que tanto Flowing Wells como Artesian Wells tienen una opinión general de la población de la comunidad del 50 % (0,50) de acuerdo, de modo que la diferencia en las proporciones de la población es igual a cero. Si se encuesta a 100 personas al azar en cada una de las dos comunidades, ¿cuál es la probabilidad de que surjan por casualidad varias diferencias en las proporciones de la muestra, debido a la aleatoriedad inherente al muestreo? La simulación toma dos muestras aleatorias de tamaño 100 de poblaciones que tienen un 50% a favor y resta una de las proporciones de la muestra de la otra. Hace esto una y otra y otra vez.
La figura 10.1 ilustra los resultados de la simulación, que es la distribución muestral de lo que se espera cuando la hipótesis nula es verdadera.
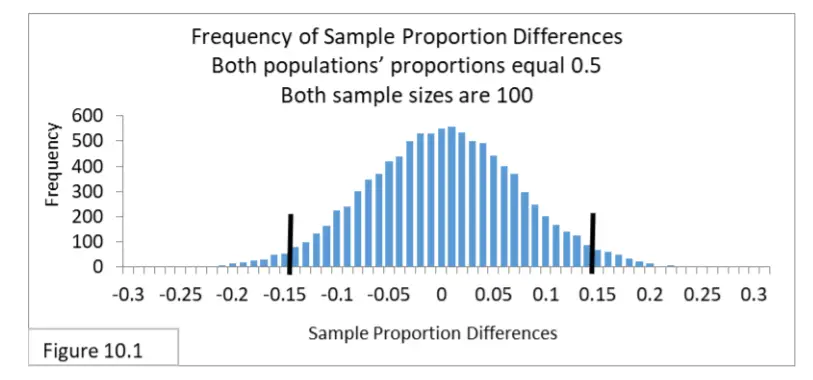 Puede ver que la distribución muestral para la diferencia entre dos proporciones muestrales es una distribución normal . Y parece que el intervalo del 95% para esta situación tiene líneas límite de -.14 y .14. Entonces, si la diferencia entre dos proporciones muestrales está dentro del intervalo -.14 a .14, entonces no rechazaremos la Hipótesis Nula . Si está fuera del intervalo, rechazaremos la hipótesis nula y diremos que la diferencia entre las dos comunidades es estadísticamente significativa . Los recursos limitados que han restringido los tamaños de muestra a 100 da un intervalo bastante amplio, donde las dos proporciones de muestra deben estar separadas por al menos 0,15 para rechazar la hipótesis nula. Las muestras pequeñas y el amplio intervalo de confianza plantean preocupaciones sobre el error de tipo II .
Puede ver que la distribución muestral para la diferencia entre dos proporciones muestrales es una distribución normal . Y parece que el intervalo del 95% para esta situación tiene líneas límite de -.14 y .14. Entonces, si la diferencia entre dos proporciones muestrales está dentro del intervalo -.14 a .14, entonces no rechazaremos la Hipótesis Nula . Si está fuera del intervalo, rechazaremos la hipótesis nula y diremos que la diferencia entre las dos comunidades es estadísticamente significativa . Los recursos limitados que han restringido los tamaños de muestra a 100 da un intervalo bastante amplio, donde las dos proporciones de muestra deben estar separadas por al menos 0,15 para rechazar la hipótesis nula. Las muestras pequeñas y el amplio intervalo de confianza plantean preocupaciones sobre el error de tipo II .
La fórmula del error estándar para la diferencia entre dos proporciones de población es Observe que los términos dentro de la raíz cuadrada siguen la misma estructura de «varianza dividida por el tamaño de la muestra» que vimos con el error estándar para una sola proporción. Ahora hay un término para cada una de las dos poblaciones. Ambas muestras tienen un tamaño de 100 y suponemos que ambas tienen una población p igual a 0,5, lo que hace que su diferencia sea igual a cero. Usando la fórmula del intervalo de confianza del 95% obtenemos Eso concuerda con la Figura 10.1; la distribución de muestreo se aproxima muy bien por la distribución z que está incorporada en la fórmula.
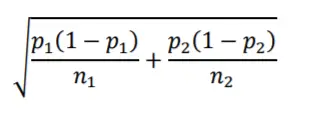
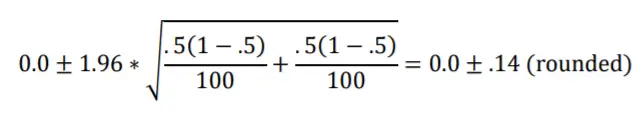
Para un análisis de ejemplo, supongamos que las proporciones binomiales de la muestra para la encuesta son: Pozos de flujo = .52 y Pozos artesianos = .44. La diferencia es .08, que está dentro del intervalo del 95%. Conclusión: No rechace la Hipótesis Nula. (Nunca aceptamos la hipótesis nula, simplemente no la rechazamos).
Realización de la encuesta para proporciones binomiales
Ahora que hemos visto la vista de pájaro, volvamos a realizar las encuestas. La primera encuesta se realiza en marzo. Vamos a analizar los datos de la encuesta utilizando el otro tipo de fórmula principal que hemos estado utilizando. Convertiremos una diferencia de proporción de muestra a la escala de error estándar. A continuación se muestra la fórmula para el error estándar de la diferencia entre dos proporciones de muestra.
̂ Supongamos que los datos de la encuesta arrojan una proporción de muestra para pozos fluidos de .52 y para pozos artesianos de .44. ¿Están estas dos proporciones de muestra lo suficientemente separadas como para que podamos decir que la diferencia es estadísticamente significativa? Primero, calcularemos el error estándar de la diferencia de proporción muestral. 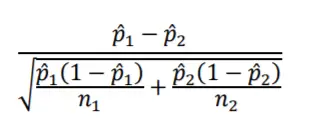
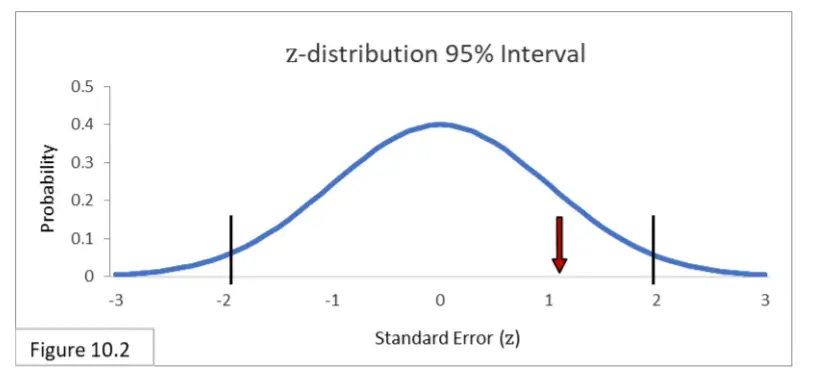
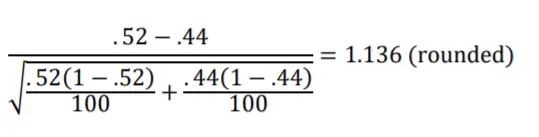 La diferencia de proporción de .08 (.52-.44) equivale a 1.136 errores estándar. Mirando ahora la Distribución Normal Estándar (distribución z) en la Figura 10.2, podemos ver que el resultado está dentro del intervalo del 95% y, por lo tanto, no rechazamos la Hipótesis Nula de que los Pozos Corrientes y los Pozos Artesianos tienen proporciones de población iguales. La diferencia de proporción de muestra de .08 no es estadísticamente significativa.
La diferencia de proporción de .08 (.52-.44) equivale a 1.136 errores estándar. Mirando ahora la Distribución Normal Estándar (distribución z) en la Figura 10.2, podemos ver que el resultado está dentro del intervalo del 95% y, por lo tanto, no rechazamos la Hipótesis Nula de que los Pozos Corrientes y los Pozos Artesianos tienen proporciones de población iguales. La diferencia de proporción de muestra de .08 no es estadísticamente significativa.
 Alguien de la organización sin fines de lucro plantea la cuestión de la importancia práctica y sugiere que el 52 % y el 44 % son lo suficientemente diferentes como para considerarse políticamente significativos. ¡Esperar! tu dices. Sin significación estadística, ¡realmente ni siquiera deberíamos estar pensando en eso! ¡Los resultados no nos permiten hablar como si las proporciones de la población fueran diferentes en absoluto! No obstante, agrega útilmente, con los tamaños de muestra pequeños, el error de tipo II parece una posibilidad real.
Alguien de la organización sin fines de lucro plantea la cuestión de la importancia práctica y sugiere que el 52 % y el 44 % son lo suficientemente diferentes como para considerarse políticamente significativos. ¡Esperar! tu dices. Sin significación estadística, ¡realmente ni siquiera deberíamos estar pensando en eso! ¡Los resultados no nos permiten hablar como si las proporciones de la población fueran diferentes en absoluto! No obstante, agrega útilmente, con los tamaños de muestra pequeños, el error de tipo II parece una posibilidad real.
Suponga que la encuesta se realiza nuevamente un mes después, en abril, y las dos proporciones binomiales de la muestra están más alejadas: .52 y .34.
En primer lugar, dado que .34 está más cerca de cero que la mayoría de las proporciones que hemos encontrado hasta ahora, verifiquemos una regla general de suposición estadística
: n ∗ p ≥ 10 y n ∗ (1 − p) ≥ 10
Con un tamaño de muestra de 100 y proporción de .34 obtenemos
100 ∗ .34 = 34 ≥ 10 y 100 ∗ (1 − .34) = 66 ≥ 10
Esta suposición se cumple cómodamente, así que calcularemos los errores estándar de la diferencia entre .52 y .34 y luego verifíquelo con la distribución z. Mirando la figura 10.3 vemos que 2.614 errores estándar está fuera del intervalo del 95%.
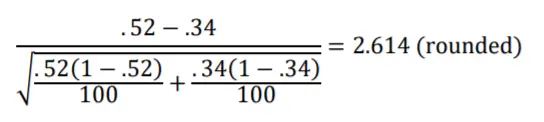
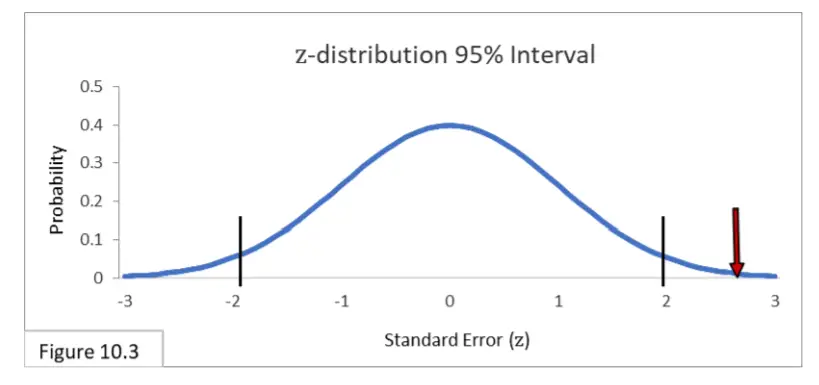 La diferencia de .18 entre .52 y .34 es estadísticamente significativa, y rechazamos la hipótesis nula de que los pozos que fluyen y los pozos artesianos tienen proporciones de población iguales. Además, parece que el 52% y el 34% son lo suficientemente diferentes como para reclamar un significado práctico, que la diferencia tiene implicaciones políticas significativas.
La diferencia de .18 entre .52 y .34 es estadísticamente significativa, y rechazamos la hipótesis nula de que los pozos que fluyen y los pozos artesianos tienen proporciones de población iguales. Además, parece que el 52% y el 34% son lo suficientemente diferentes como para reclamar un significado práctico, que la diferencia tiene implicaciones políticas significativas.
A continuación, digamos que para la encuesta del mes siguiente, en mayo, se comprometen recursos adicionales para que se puedan recolectar muestras más grandes. Los valores estadísticos de la muestra son los mismos que hace dos meses, en marzo, proporciones de muestra de 0,52 y 0,44, pero ahora los tamaños de muestra son 1000. Al observar la figura 10.4, vemos que 3,592 errores estándar está fuera del intervalo del 95 %.
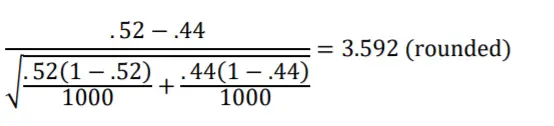
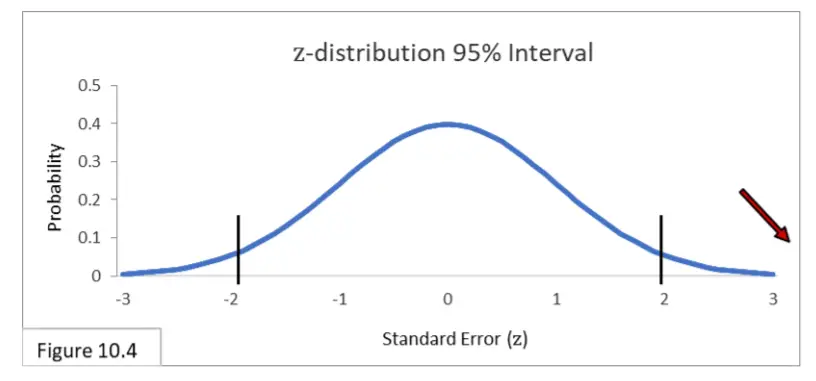 (Está fuera del gráfico que se muestra aquí, pero la distribución z en sí misma en realidad va de infinito negativo a infinito positivo). Con tamaños de muestra de 1000, la diferencia de 0,08 entre 0,52 y 0,44 es estadísticamente significativa, y rechazamos la Hipótesis Nula de que los Pozos Corrientes y los Pozos Artesianos tienen proporciones binomiales poblacionales iguales. Si bien la diferencia de .08 no fue estadísticamente significativa en marzo con tamaños de muestra de 100, es estadísticamente significativa en mayo con tamaños de muestra de 1000. El poder estadístico adicional debido al tamaño de muestra más grande hace eso. Y aunque siempre es posible que se haya producido un error de tipo I cada vez que rechazamos una hipótesis nula, nuestra experiencia en los últimos meses nos convence de que la diferencia de este mes probablemente sea real. No está claro, sin embargo, si el 52% y el 44% son lo suficientemente diferentes como para tener serias implicaciones políticas. Quizás debamos preguntar a algunos politólogos si creen que estos resultados de encuestas estadísticamente significativos tienen algún significado práctico.
(Está fuera del gráfico que se muestra aquí, pero la distribución z en sí misma en realidad va de infinito negativo a infinito positivo). Con tamaños de muestra de 1000, la diferencia de 0,08 entre 0,52 y 0,44 es estadísticamente significativa, y rechazamos la Hipótesis Nula de que los Pozos Corrientes y los Pozos Artesianos tienen proporciones binomiales poblacionales iguales. Si bien la diferencia de .08 no fue estadísticamente significativa en marzo con tamaños de muestra de 100, es estadísticamente significativa en mayo con tamaños de muestra de 1000. El poder estadístico adicional debido al tamaño de muestra más grande hace eso. Y aunque siempre es posible que se haya producido un error de tipo I cada vez que rechazamos una hipótesis nula, nuestra experiencia en los últimos meses nos convence de que la diferencia de este mes probablemente sea real. No está claro, sin embargo, si el 52% y el 44% son lo suficientemente diferentes como para tener serias implicaciones políticas. Quizás debamos preguntar a algunos politólogos si creen que estos resultados de encuestas estadísticamente significativos tienen algún significado práctico.
Siguiente : El resto del iceberg (frecuentista)
Referencias
JE Kotteman. Análisis Estadístico Ilustrado – Fundamentos . Publicado vía Copyleft . Eres libre de copiar y distribuir el contenido de este artículo.

