Contenido de este artículo
Actualizado el 31 de agosto de 2021, por Luis Benites.
Previous : Errores Tipo I y Tipo II .
Los siguientes seis estudios de casos estadísticos breves exploran el error de tipo I y el error de tipo II en diversas circunstancias. Los casos impares se concentran en el error de tipo I. Estos casos ilustran que la frecuencia esperada del error de tipo I no cambia en las distintas circunstancias. Los casos con números pares se concentran en el error de tipo II e ilustran que la frecuencia esperada del error de tipo II cambia en las distintas circunstancias. Tenga en cuenta que para todos estos casos, nosotros, que somos sabelotodos, sabemos cuáles son los porcentajes reales de la población, ¡pero los encuestadores no!
Estudios de casos estadísticos #1
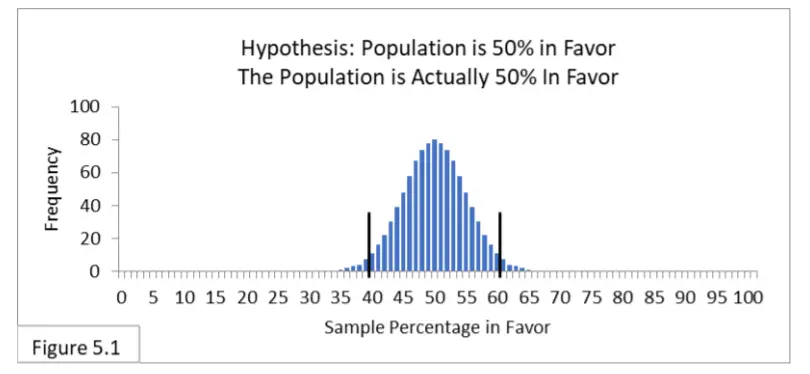 Haciendo referencia a la figura 5.1, suponga que el 50 % de la población está a favor de una nueva política de salud pública y que 1000 encuestadores encuestan a la población mediante un muestreo aleatorio de tamaño de muestra 100. Los 1000 encuestadores plantean la hipótesis de que el 50 % de la población está a favor y utilizan el intervalo de confianza del 95% apropiado que abarca del 40% al 60%. Espere que el 95% (dentro del intervalo) no rechace la hipótesis. No lo saben, pero de hecho tienen razón. Espere que el 5% (fuera del intervalo) rechace la hipótesis nula y sufra un error de tipo I. Ellos no lo saben, pero de hecho son
Haciendo referencia a la figura 5.1, suponga que el 50 % de la población está a favor de una nueva política de salud pública y que 1000 encuestadores encuestan a la población mediante un muestreo aleatorio de tamaño de muestra 100. Los 1000 encuestadores plantean la hipótesis de que el 50 % de la población está a favor y utilizan el intervalo de confianza del 95% apropiado que abarca del 40% al 60%. Espere que el 95% (dentro del intervalo) no rechace la hipótesis. No lo saben, pero de hecho tienen razón. Espere que el 5% (fuera del intervalo) rechace la hipótesis nula y sufra un error de tipo I. Ellos no lo saben, pero de hecho son
incorrectos. Simplemente obtuvieron una muestra aleatoria engañosa . El tipo II es irrelevante porque la hipótesis es de hecho correcta (sin que ninguno de los encuestadores lo sepa).
Ahora imagina que eres uno de esos topógrafos. Hay un 95 % de posibilidades de que seas uno de aquellos cuya muestra aleatoria te llevó a la conclusión correcta, y un 5 % de posibilidades de que seas uno de aquellos cuya muestra aleatoria te llevó a una conclusión incorrecta (Error tipo I) .
Estudios de casos estadísticos: Caso 2
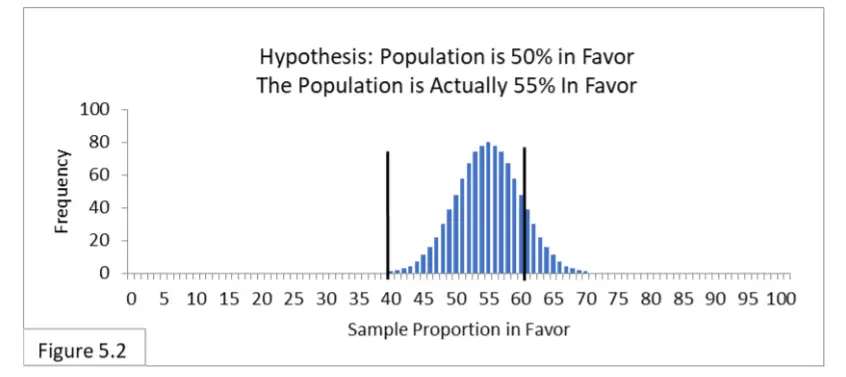 Haciendo referencia a la figura 5.2, suponga que el 55 % de la población está a favor de una nueva política de salud pública y que 1000 encuestadores encuestan a la población utilizando un muestreo aleatorio con un tamaño de muestra de 100. Los 1000 encuestadores plantean la hipótesis de que el 50 % de la población está a favor y utilizan el método adecuado. Intervalo de confianza del 95% que va del 40% al 60%. Espere que alrededor del 85% (dentro del intervalo) no rechace la hipótesis y, por lo tanto, sufra el error de tipo II. Ellos no lo saben, pero de hecho son incorrectos. Espere alrededor del 15% (fuera del intervalo) para rechazar la hipótesis. No lo saben, pero de hecho tienen razón.
Haciendo referencia a la figura 5.2, suponga que el 55 % de la población está a favor de una nueva política de salud pública y que 1000 encuestadores encuestan a la población utilizando un muestreo aleatorio con un tamaño de muestra de 100. Los 1000 encuestadores plantean la hipótesis de que el 50 % de la población está a favor y utilizan el método adecuado. Intervalo de confianza del 95% que va del 40% al 60%. Espere que alrededor del 85% (dentro del intervalo) no rechace la hipótesis y, por lo tanto, sufra el error de tipo II. Ellos no lo saben, pero de hecho son incorrectos. Espere alrededor del 15% (fuera del intervalo) para rechazar la hipótesis. No lo saben, pero de hecho tienen razón.
El error tipo I es irrelevante porque la hipótesis es de hecho incorrecta (sin que ninguno de los encuestadores lo sepa). Puede parecer impactante, pero debido a que el 55 % está tan cerca del 50 % y debido a que 100 es un tamaño de muestra algo pequeño, ¡se espera que aproximadamente el 85 % de los encuestadores lleguen a una conclusión incorrecta!
Ahora imagina que eres uno de esos topógrafos. Hay un 15 % de posibilidades de que seas uno de aquellos cuya muestra aleatoria te llevó a la conclusión correcta, y un 85 % de posibilidades de que seas uno de aquellos cuya muestra aleatoria te llevó a una conclusión incorrecta (Error de tipo II) .
Caso 3
Aumentemos el tamaño de la muestra .
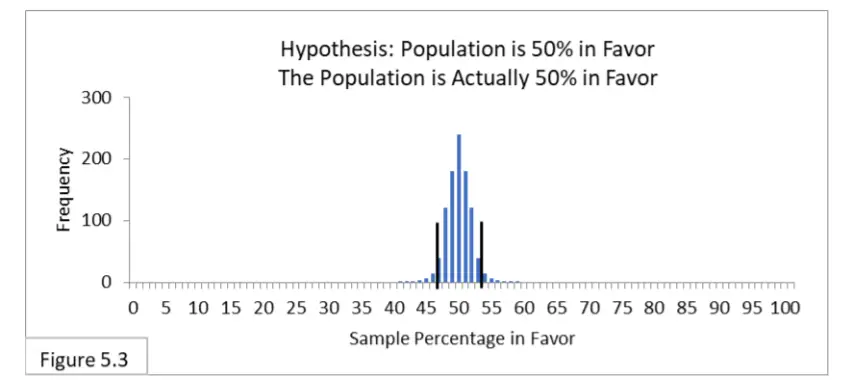 Con referencia a la figura 5.3, suponga que una población está 50 % a favor de una nueva política de salud pública y 1000 encuestadores encuestan a la población utilizando un muestreo aleatorio con un tamaño de muestra de 1000. Los 1000 encuestadores plantean la hipótesis de que la población está 50 % a favor. Nada ha cambiado con respecto al error de tipo I porque todos siguen usando un intervalo del 95 %, que ahora se extiende del 47 % al 53 %, y la hipótesis es cierta. Todavía esperamos que el 95% sea correcto y el 5% incorrecto. El error tipo II es irrelevante porque la hipótesis es realmente cierta. Ahora imagina que eres uno de esos topógrafos. Hay un 95 % de posibilidades de que seas uno de aquellos cuya muestra aleatoria te llevó a la conclusión correcta, y un 5 % de posibilidades de que seas uno de aquellos cuya muestra aleatoria te llevó a una conclusión incorrecta (Error tipo I) .
Con referencia a la figura 5.3, suponga que una población está 50 % a favor de una nueva política de salud pública y 1000 encuestadores encuestan a la población utilizando un muestreo aleatorio con un tamaño de muestra de 1000. Los 1000 encuestadores plantean la hipótesis de que la población está 50 % a favor. Nada ha cambiado con respecto al error de tipo I porque todos siguen usando un intervalo del 95 %, que ahora se extiende del 47 % al 53 %, y la hipótesis es cierta. Todavía esperamos que el 95% sea correcto y el 5% incorrecto. El error tipo II es irrelevante porque la hipótesis es realmente cierta. Ahora imagina que eres uno de esos topógrafos. Hay un 95 % de posibilidades de que seas uno de aquellos cuya muestra aleatoria te llevó a la conclusión correcta, y un 5 % de posibilidades de que seas uno de aquellos cuya muestra aleatoria te llevó a una conclusión incorrecta (Error tipo I) .
Estudios de casos estadísticos: Caso 4
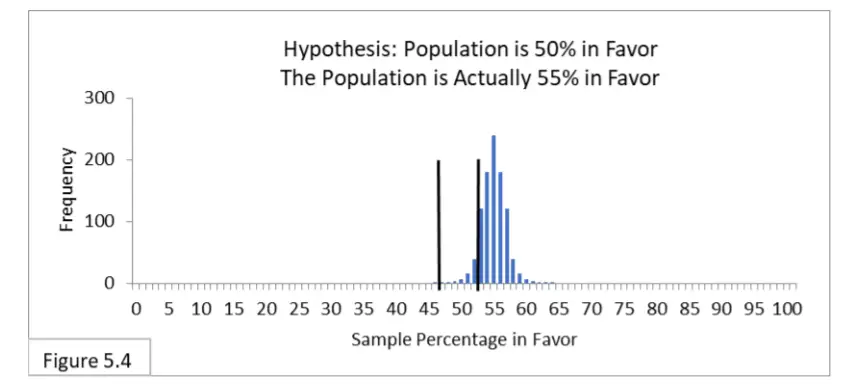 Haciendo referencia a la Figura 5.4, suponga que el 55 % de la población está a favor de una nueva política de salud pública y que 1000 encuestadores encuestan a la población utilizando un muestreo aleatorio de tamaño de muestra de 1000. Su hipótesis es que el 50 % de la población está a favor de la nueva política, y utilizan el correspondiente intervalo de 95% de 47% a 53%. Debido al aumento del tamaño de la muestra (mayor poder), ahora esperamos que aproximadamente el 90 % de los encuestadores estén en lo correcto (en lugar del 15 % en el caso 2). Y esperamos que alrededor del 10 % sea incorrecto y sufra un error de tipo II (en lugar del 85 % en el caso 2). Eso está mucho mejor. El error tipo I es irrelevante porque la hipótesis es en realidad falsa. Ahora imagina que eres uno de esos topógrafos. Hay un 90 % de posibilidades de que seas uno de aquellos cuya muestra aleatoria te llevó a la conclusión correcta,
Haciendo referencia a la Figura 5.4, suponga que el 55 % de la población está a favor de una nueva política de salud pública y que 1000 encuestadores encuestan a la población utilizando un muestreo aleatorio de tamaño de muestra de 1000. Su hipótesis es que el 50 % de la población está a favor de la nueva política, y utilizan el correspondiente intervalo de 95% de 47% a 53%. Debido al aumento del tamaño de la muestra (mayor poder), ahora esperamos que aproximadamente el 90 % de los encuestadores estén en lo correcto (en lugar del 15 % en el caso 2). Y esperamos que alrededor del 10 % sea incorrecto y sufra un error de tipo II (en lugar del 85 % en el caso 2). Eso está mucho mejor. El error tipo I es irrelevante porque la hipótesis es en realidad falsa. Ahora imagina que eres uno de esos topógrafos. Hay un 90 % de posibilidades de que seas uno de aquellos cuya muestra aleatoria te llevó a la conclusión correcta,
conclusión incorrecta (Error Tipo II). ¡Probabilidades mucho mejores que en el Caso 2!
Caso 5
Hagamos nuestro criterio de Error Tipo I más estricto. El error de tipo I es más temido que el error de tipo II, y como logramos, en el caso 4, reducir la tasa esperada de error de tipo II a alrededor del 10 %, aprovechemos eso y hagamos que nuestro criterio de error de tipo I sea más estricto, sabiendo muy bien que aumentará la probabilidad de error de tipo II. Haciendo referencia a la figura 5.5, suponga que el 50 % de la población está a favor de una nueva política de salud pública y que 1000 encuestadores encuestan a la población mediante un muestreo aleatorio con un tamaño de muestra de 1000. Su hipótesis es que el 50 % de la población está a favor de la nueva política. Ahora van a utilizar intervalos del 99 %, que van del 46 % al 54 %. Ahora esperamos que el 99% de los encuestadores estén en lo correcto y el 1% en lo incorrecto. El error tipo II es irrelevante.
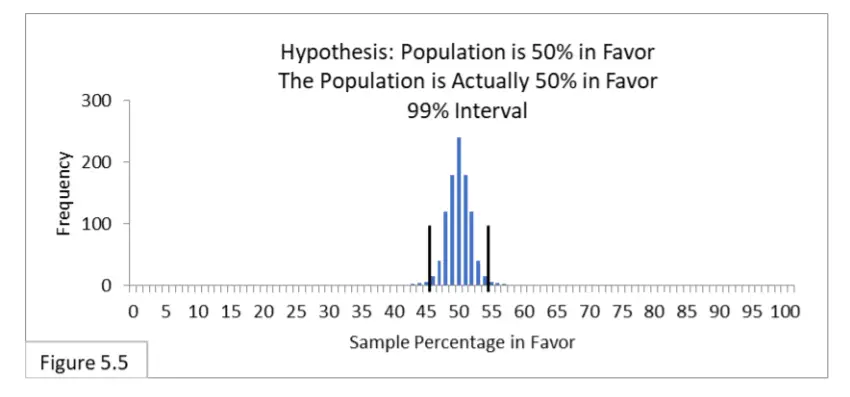
Ahora imagina que eres uno de esos topógrafos. Hay un 99 % de posibilidades de que seas uno de aquellos cuya muestra aleatoria te llevó a la conclusión correcta, y un 1 % de posibilidades de que seas uno de aquellos cuya muestra aleatoria te llevó a una conclusión incorrecta (Error tipo I) .
Estudios de casos estadísticos: Caso 6
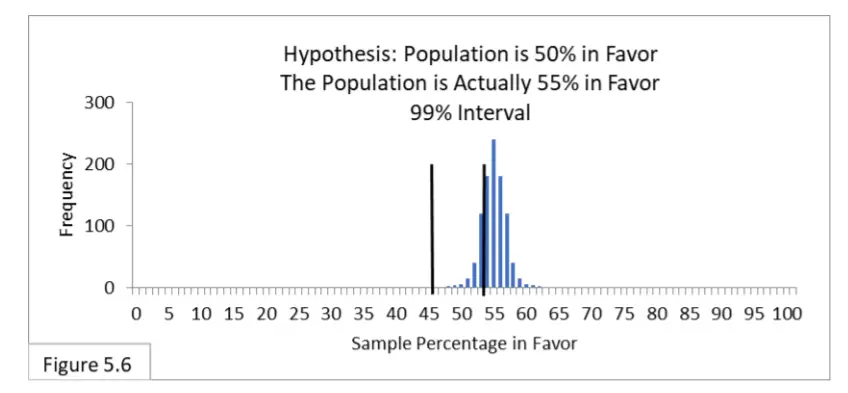 Haciendo referencia a la figura 5.6, suponga que el 55 % de la población está a favor de una nueva política de salud pública y que 1000 encuestadores encuestan a la población utilizando un muestreo aleatorio de tamaño de muestra de 1000. Su hipótesis es que el 50 % de la población está a favor de la nueva política, y utilizan el correspondiente intervalo de 99% de 46% a 54%. Debido al criterio de error tipo I más estricto y su intervalo más amplio del 99 %, ahora esperamos que aproximadamente el 70 % de los encuestadores estén en lo correcto (en lugar del 90 % en el Caso 4). Y esperamos que alrededor del 30 % sea incorrecto y sufra un error de tipo II (en lugar del 10 % en el caso 4). El error tipo I
Haciendo referencia a la figura 5.6, suponga que el 55 % de la población está a favor de una nueva política de salud pública y que 1000 encuestadores encuestan a la población utilizando un muestreo aleatorio de tamaño de muestra de 1000. Su hipótesis es que el 50 % de la población está a favor de la nueva política, y utilizan el correspondiente intervalo de 99% de 46% a 54%. Debido al criterio de error tipo I más estricto y su intervalo más amplio del 99 %, ahora esperamos que aproximadamente el 70 % de los encuestadores estén en lo correcto (en lugar del 90 % en el Caso 4). Y esperamos que alrededor del 30 % sea incorrecto y sufra un error de tipo II (en lugar del 10 % en el caso 4). El error tipo I
es irrelevante.
Ahora imagina que eres uno de esos topógrafos. Hay un 70 % de posibilidades de que seas uno de aquellos cuya muestra aleatoria te llevó a la conclusión correcta, y un 30 % de posibilidades de que seas uno de aquellos cuya muestra aleatoria te llevó a una conclusión incorrecta (Error de tipo II) . Con un tamaño de muestra de 1000, ¿cuál elegiría, las tasas de errores de tipo I y II de 5 % y 10 % como en los casos 3 y 4, o 1 % y 30 % como en los casos 5 y 6? Bueno, eso depende de lo costoso que sea cometer cada tipo de error. Y eso depende del contexto. Si las repercusiones del error de tipo I son mucho peores que las del error de tipo II, elegiría el 1 % y el 30 %. Si no, elegirías 5% y 10%. O bien, podría pagar para obtener muestras aún más grandes e intentar obtener el 1 % y el 10 % para obtener lo mejor de ambos. (Pero recuerde, solo hemos considerado el error de tipo II en los casos en que la población está a favor en un 55 %.
El resultado final: el tamaño de la muestra es una forma importante de administrar las tasas de error. Los tamaños de muestra más grandes en los estudios de casos de estadísticas le permiten hacer que su nivel de error tipo I sea más estricto, si lo desea, al mismo tiempo que se asegura de que su nivel de error tipo II siga siendo razonable.
Terminología y notación para estudios de casos estadísticos: Matemáticamente, la probabilidad de error tipo I se denota con la letra griega alfa minúscula, α. El nivel de porcentaje de confianza, al que nos hemos estado refiriendo mucho, es (1 – α) * 100 %. Entonces, un nivel alfa de 0.05 es equivalente a un nivel de confianza del 95%. La probabilidad de error de tipo II se denota con la letra griega minúscula beta, β. El poder estadístico es 1 – β (no convertido en porcentaje).
Así, por ejemplo, un nivel beta de 0,20 equivale a un nivel de potencia de 0,80.
Siguiente : La Hipótesis Central
Referencias
JE Kotteman. Análisis Estadístico Ilustrado – Fundamentos . Publicado vía Copyleft . Eres libre de copiar y distribuir el contenido de este artículo.
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo:
