Contenido de este artículo
Actualizado el 20 de febrero de 2022, por Luis Benites.
La prueba de bondad de ajuste se utiliza para comprobar si los datos de la muestra se ajustan a una distribución de una determinada población (es decir, una población con una distribución normal o una con una distribución de Weibull ). En otras palabras, le dice si los datos de su muestra representan los datos que esperaría encontrar en la población real. Las pruebas de bondad de ajuste comúnmente utilizadas en estadística son:
La prueba de bondad de ajuste de Chi cuadrado
Mire el video para obtener una descripción general de las pruebas de chi-cuadrado:
Introducción a la prueba de chi-cuadrado Mira este video en YouTube .
¿No puedes ver el vídeo? Haga clic aquí
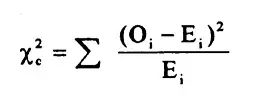
La fórmula de chi-cuadrado.
La prueba de chi-cuadrado es la más común de las pruebas de bondad de ajuste y es la que encontrará en estadísticas AP o estadísticas elementales . El chi cuadrado se puede usar para distribuciones discretas como la distribución binomial y la distribución de Poisson , mientras que las pruebas de bondad de ajuste de Kolmogorov-Smirnov y Anderson-Darling solo se pueden usar para distribuciones continuas .
Dos desventajas potenciales de chi cuadrado son:
- La prueba de chi cuadrado solo se puede usar para datos colocados en clases (contenedores). Si tiene datos no agrupados, deberá hacer una tabla de frecuencia o un histograma antes de realizar la prueba.
- Otra desventaja de la prueba de chi-cuadrado es que requiere un tamaño de muestra suficiente para que la aproximación de chi-cuadrado sea válida.
Hay otro tipo de prueba de chi-cuadrado, llamada prueba de independencia de chi-cuadrado . Los dos a veces se confunden, pero son bastante diferentes.
- La prueba de chi-cuadrado para la independencia compara dos conjuntos de datos para ver si existe una relación.
- La bondad de ajuste chi-cuadrado es ajustar una variable categórica a una distribución.
Ambas pruebas usan la estadística y distribución chi-cuadrado. Para obtener más información sobre cómo calcular la estadística chi cuadrada, consulte:
La estadística de prueba chi cuadrada (incluye cálculos): ¿Qué es una estadística chi cuadrada?
Ejecución de la prueba
Por lo general, esta prueba se ejecuta mediante software. La hipótesis nula para la prueba de bondad de ajuste chi-cuadrado es que los datos provienen de una distribución específica. La hipótesis alternativa es que los datos no provienen de una distribución específica.
Para interpretar la prueba, deberá elegir un nivel alfa (1%, 5% y 10% son comunes). La prueba de chi-cuadrado devolverá un valor p . Si el valor p es pequeño (menor que el nivel de significancia), puede rechazar la hipótesis nula de que los datos provienen de la distribución especificada.
Pruebas de bondad de ajuste menos comunes utilizadas en estadísticas elementales
Kolmogorov-Smirnov
Aunque esto se denomina prueba de normalidad, en realidad no le dice si una muestra en particular probablemente proviene de una población normal. En cambio, le dirá cuándo es poco probable que tenga una distribución normal . Una ventaja de esta prueba es que no hace suposiciones sobre la distribución de datos. Una muestra se puede comparar con una distribución utilizando una prueba K-S de una muestra o una prueba K-S de dos muestras. La prueba generalmente se realiza utilizando un software (como SPSS ), porque los valores críticos deben calcularse para cada distribución y encontrar las tablas de valores críticos no es una tarea fácil. La prueba generalmente se recomienda para muestras grandes de más de 2000. Para muestras más pequeñas, use Shapiro-Wilk.
anderson-cariño
Esta prueba es una modificación de Kolmogorov-Smirnov. Es más sensible a las desviaciones en las colas de una distribución. Al igual que Kolmogorov-Smirnov, esta prueba le dirá cuándo es poco probable que tenga una distribución normal y normalmente se ejecuta con software estadístico.
Shapiro-Wilk
Esta prueba calcula un valor W que le indicará si una muestra aleatoria proviene de una población distribuida normalmente. La prueba se recomienda para muestras hasta n=2000.
Referencias
Beyer, WH CRC Standard Mathematical Tables, 31ª ed. Boca Raton, FL: CRC Press, págs. 536 y 571, 2002.
Dodge, Y. (2008). La Enciclopedia Concisa de Estadística . Saltador.
Gonick, L. (1993). La guía de dibujos animados de estadísticas . Harper Perennial.
Vogt, WP (2005). Diccionario de estadística y metodología: una guía no técnica para las ciencias sociales . SABIO.
