Contenido de este artículo
- 0
- 0
- 0
- 0
Actualizado el 2 de septiembre de 2021, por Luis Benites.
La prueba Chi-Cuadrado de Normalidad nos permite comprobar si un modelo o teoría sigue o no una distribución aproximadamente normal .
La prueba de normalidad Chi-Cuadrado no es tan poderosa como otras pruebas más específicas (como Lilliefors ). Aún así, es una forma útil y rápida de verificar la normalidad, especialmente cuando tiene un conjunto discreto de puntos de datos.
Cómo utilizar la prueba de chi-cuadrado para la normalidad.
Para aplicar la prueba de normalidad de chi-cuadrado a cualquier conjunto de datos, deje que su hipótesis nula sea que sus datos se muestrean a partir de una distribución normal y aplique la prueba de bondad de ajuste de chi-cuadrado . Dada su media y desviación estándar , deberá calcular los valores esperados bajo la distribución normal para cada punto de datos. Luego usa la fórmula para encontrar la estadística de chi-cuadrado. Compare esto con el valor crítico de chi-cuadrado de una tabla de chi-cuadrado, dados sus grados de libertad y el nivel alfa deseado . Si su estadística de chi-cuadrado es mayor que el valor de la tabla, puede concluir que sus datos no son
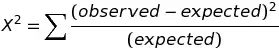normal.
Cuándo no utilizar la prueba de normalidad Chi-Cuadrado
La prueba de normalidad de Chi cuadrado solo se puede utilizar si:
- Su valor esperado para el número de observaciones de muestra para cada nivel es mayor que 5
- Sus datos se muestrean aleatoriamente
- La variable que estás estudiando es categórica .
Si su variable es continua , deberá agrupar los datos antes de usar la prueba de chi-cuadrado para la normalidad.
Alternativas a la prueba de normalidad Chi-Cuadrado
Las alternativas a la prueba de normalidad de chi-cuadrado incluyen:
- La prueba de Kolmogorov-Smirnov (KS)
- La prueba de KS corregida de Lilliefors
- La prueba de Shapiro-Wilk
- La prueba de Anderson-Darling
- La prueba de Cramer-von Mises
- La prueba ómnibus D’Agostino-Pearson
- La prueba de Jarque-Bera
Todas estas pruebas tienen diferentes fortalezas y debilidades, pero la prueba de Shapiro Wilk puede tener la mejor potencia para cualquier significado dado.
Fuentes:
Pruebas de normalidad para el análisis estadístico: una guía para no estadísticos
<a href=»https://web.archive.org/web/20150630110326/http://instatmy.org.my/downloads/e-jurnal%202 /3.pdf» target=»_blank»Comparaciones de potencia de las pruebas de Shapiro-Wilk, Kolmogorov-Smirnov, Lilliefors y Anderson-Darling. Journal of Statistical Modeling and Analytics
Stattrek Bondad of Fit Test
Stat 452 Estadísticas: métodos continuos
Chi-cuadrado Goodness Test en SPSS Statistics
Redactor del artículo
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo:
