Contenido de este artículo
- 0
- 0
- 0
- 0
Actualizado el 21 de octubre de 2021, por Luis Benites.
<< Artículo anterior: ¿Qué es ANCOVA ?
¿Qué es MANCOVA?
MANCOVA (Análisis Multivariante de Covarianza) es la contraparte multivariante de ANCOVA . MANCOVA te dice si hay diferencias de medias estadísticamente significativas entre los grupos. En otras palabras, le dice si las diferencias de grupo probablemente ocurrieron por casualidad o si hay una tendencia repetible .
Mira el video para una introducción:
¿Qué es MANCOVA? Mira este video en YouTube .
¿No puedes ver el vídeo? Haga clic aquí
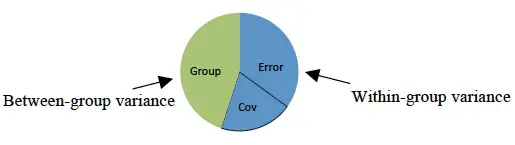
Las covariables se controlan en MANCOVA. Imagen: Makingstats|Wikimedia Commons
MANCOVA elimina los efectos de una o más covariables de su modelo ; Esto le permite ver el verdadero efecto de sus variables independientes en sus variables dependientes sin interferencias no deseadas. Esta prueba sobrecargada tiene un costo: los tamaños de muestra MANCOVA requeridos son mucho más grandes que otras pruebas. Es posible que esto no valga la pena el tiempo y los gastos adicionales; la mayoría de las veces, un MANOVA (es decir, la misma prueba sin mirar las covariables) puede ser más poderoso.
Tipos
- Un MANCOVA unidireccional necesita al menos cuatro variables: una variable independiente con dos o más grupos (niveles o factores) más dos o más variables dependientes y una o más covariables.
- Un MANCOVA de dos vías incluye dos variables independientes.
Covariables/Covarianza definida
La covarianza es una medida de cuánto varían juntas dos variables aleatorias . Es similar a la varianza, pero donde la varianza te dice cómo varía una sola variable, la covarianza te dice cómo varían dos variables juntas. Una covariable puede ser una de estas dos variables. Es cualquier variable que afecta la forma en que sus variables independientes actúan sobre sus variables dependientes. Por ejemplo, las variables de confusión son covariables.
suposiciones
Los supuestos para MANCOVA son los mismos que los supuestos para MANOVA, con la adición de un par más para la covarianza. Como era de esperar con una prueba compleja (en comparación con una prueba mucho más simple como una prueba z ), estas suposiciones son largas y algo complejas. Esta es una de las razones por las que estas pruebas casi siempre se realizan con software, ya que la mayoría del software estadístico probará estos supuestos antes de ejecutar la prueba.
- Las covariables y las variables dependientes son continuas y de razón / ordinales .
- Las matrices de covarianza deben ser iguales (reduce el error de tipo I ).
- Las variables independientes son categóricas .
- Independencia de las variables: las variables no se influyen entre sí.
- Muestreo aleatorio : los datos se recopilaron mediante un método de selección aleatoria.
- Normalidad : las variables dependientes siguen una distribución normal (multinomial) para cada grupo.
- Ausencia de multicolinealidad : las variables dependientes no deben estar significativamente correlacionadas.
- Homogeneidad de varianza entre grupos.
Las covariables que elija deben estar correlacionadas con las variables dependientes. Esto se puede probar antes de su inclusión en MANCOVA con análisis de correlación. Las mejores variables dependientes, por otro lado, no están correlacionadas entre sí.
Diferencias entre MANCOVA y otras pruebas similares
MANCOVA, MANOVA, ANOVA, ANCOVA: todo puede ser un poco confuso para recordar cuál es cuál. Sin embargo, todas las pruebas se pueden considerar como variantes de MANCOVA, si recuerda que la » M » en MANCOVA significa M últiple y la » C » significa C ovariable. Las pruebas pueden ser pensadas como un MACOVA…
- ANOVA : … sin múltiples variables dependientes y covariables (de ahí la falta de M y C).
- ANCOVA : …sin múltiples variables dependientes (de ahí la falta de M).
- MANOVA : …sin covariables (de ahí la falta de C).
Artículos relacionados:
Referencias :
Tabachnick, BG y Fidell, LS (1983). Uso de estadísticas multivariadas. Nueva York: Harper & Row.
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo:
