Actualizado por ultima vez el 20 de octubre de 2021, por Luis Benites.
Comparación de Medios Técnicas
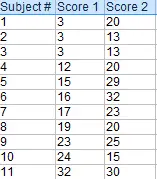
La comparación de las pruebas de medios le ayuda a determinar si sus grupos tienen medios similares.
Hay muchos casos en estadística en los que querrá comparar las medias de dos poblaciones o muestras . La técnica que utilice depende del tipo de datos que tenga y de cómo se agrupen esos datos.
Las cuatro formas principales de comparar las medias de los datos que se supone que se distribuyen normalmente son:
- Prueba T para muestras independientes. Utilice la prueba t de muestras independientes cuando desee comparar las medias de dos conjuntos de datos que son independientes entre sí. Haga clic aquí para ver un artículo paso a paso .
- Prueba T de una muestra. Elija esto cuando desee comparar medias entre un conjunto de datos y una constante específica (como la media de una distribución normal hipotética). Haga clic aquí para ver un artículo paso a paso .
- Prueba T de muestras pareadas . Use esta prueba si tiene un grupo evaluado en dos momentos diferentes. En otras palabras, tiene dos medidas en el mismo artículo, persona o cosa. Los grupos están “emparejados” porque existen conexiones intrínsecas entre ellos (es decir, no son independientes ). Esta comparación de medias se usa a menudo para grupos de pacientes antes y después del tratamiento, o para estudiantes evaluados antes y después de la remediación. Haga clic aquí para ver un artículo paso a paso .
- Análisis de varianza de una vía (ANOVA) . Aunque no es realmente una prueba de comparación de medias, ANOVA es la opción principal cuando se tienen más de dos niveles de variable independiente . Por ejemplo, si su variable independiente fuera «marca de café», sus niveles podrían ser Starbucks, Peets y Trader Joe’s. Use esta prueba cuando tenga un grupo de personas divididas aleatoriamente en grupos más pequeños y completando diferentes tareas (como beber café diferente).
Datos no normales
Si tiene datos que no son normales (o si no sabe de qué distribución provienen), no puede usar ninguna de las pruebas anteriores para comparar las medias. Debe usar una prueba no paramétrica (no paramétrica básicamente significa que no conoce los parámetros de la distribución ):
- Para muestras independientes, utilice la prueba U de Mann-Whitney . Esta prueba es esencialmente la misma que la prueba t para muestras independientes.
- Para grupos emparejados, utilice el rango con signos de Wilcoxon . Esta prueba compara medianas , no medias.
Referencias
Beyer, WH CRC Standard Mathematical Tables, 31ª ed. Boca Raton, FL: CRC Press, págs. 536 y 571, 2002.
Everitt, BS; Skrondal, A. (2010), The Cambridge Dictionary of Statistics , Cambridge University Press.
Vogt, WP (2005). Diccionario de estadística y metodología: una guía no técnica para las ciencias sociales . SABIO.
Wheelan, C. (2014). Estadísticas desnudas . WW Norton y compañía
