Supuestos MANCOVA

Actualizado por ultima vez el 14 de septiembre de 2021, por Luis Benites.

El análisis multivariado de covarianza (MANCOVA) se utiliza para probar la significación estadística de los efectos de una o más variables independientes sobre dos o más variables dependientes , después de controlar las covariables .

MANCOVA, al igual que otras pruebas estadísticas, requiere que los datos cumplan con varios supuestos importantes para obtener resultados significativos. Los supuestos son los mismos para MANOVA , con requisitos adicionales relacionados con las covariables. Esto conduce a una larga lista de suposiciones, lo que puede hacer que el análisis sea un poco abrumador para los principiantes. Sin embargo, si está utilizando software (como SPSS), la prueba de suposiciones se convierte en un desafío menor y es la razón principal por la que MANCOVA rara vez se realiza a mano.

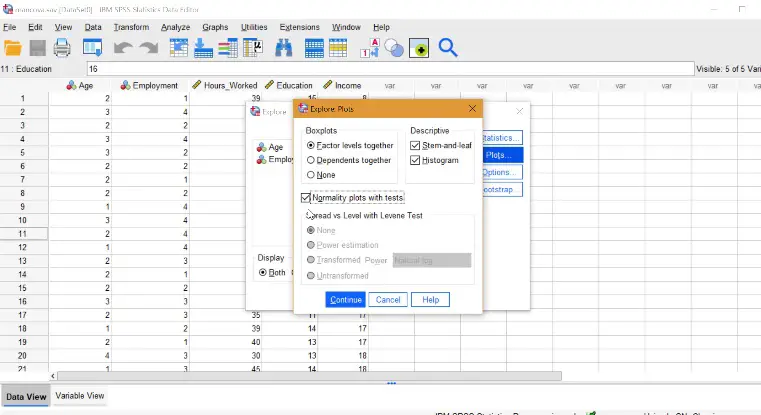
Prueba de supuestos MANCOVA en SPSS.

¿Qué son los Supuestos MANCOVA?

Los supuestos básicos son:

1. Nivel de Medición: Las variables independientes deben ser categóricas ; Las variables dependientes deben medirse en el nivel de intervalo o superior (es decir , variables de escala o variables continuas ). Las covariables tienen más flexibilidad y pueden ser continuas , dicotómicas u ordinales .
2. Independencia de las observaciones : Las observaciones deben ser independientes de todas las demás observaciones; Si sus datos se extrajeron utilizando un método de muestreo aleatorio , se cumple esta suposición.
3. Las variables dependientes deben distribuirse normalmente dentro de los grupos.
4. Debe cumplirse la homogeneidad de varianzas para cada variable dependiente. En otras palabras, las varianzas en los grupos de diferencia deben ser las mismas.
5. Homogeneidad de covarianzas : La matriz de intercorrelación entre variables dependientes debe ser igual para todos los niveles de la variable independiente.
6. Debe haber una relación lineal significativa entre la variable dependiente y la covariable [1].
7. La pendiente de la línea de regresión debe ser la misma en cada grupo.

Si desea probar estas suposiciones, use el software: Consulte: Cómo ejecutar un MANCOVA en SPSS .

Efecto de violar los supuestos de MANCOVA

Si sus datos violan gravemente las suposiciones, sus valores p pierden sentido y abre su investigación a un mayor riesgo de errores de tipo I y tipo II .

La violación de algunos supuestos, como la normalidad multivariada, genera un efecto mínimo en su análisis; La prueba F es muy robusta a las desviaciones de la normalidad. Sin embargo, la suposición de normalidad aún debe tenerse en cuenta para asegurarse de que sus datos no se desvíen por completo de la suposición. En general, si su curtosis es mayor que 0, el estadístico F será demasiado pequeño para rechazar la hipótesis nula [2].

Otras violaciones son mucho más problemáticas, incluida la violación del supuesto de independencia, lo que conduce a una mayor probabilidad de error de tipo I en la estadística F. También interfiere con los errores estándar de las medias y las inferencias sobre ellos.

La violación de la suposición de homogeneidad de las matrices de varianza-covarianza conduce a una gran cantidad de problemas, incluido el aumento de la probabilidad de errores de Tipo I y Tipo II. Si tiene un diseño desequilibrado , con una proporción de 1:2 o más, las tasas de error de tipo I aumentan drásticamente, incluso con una heterogeneidad leve [3].

Referencias

[1] Siri, F. et. Alabama. (2018). Las artes y el cerebro . Recuperado el 12 de octubre de 2021 de: https://www.sciencedirect.com/topics/medicine-and-dentistry/multivariate-analysis-of-covariance
[2] ANOVA/MANOVA.
Recuperado el 12 de octubre de 2021 de: https://sites.oxy.edu/lengyel/m150/textbook/stanman.html#assumptions
[3] MANOVA y MANCOVA. Recuperado el 12 de octubre de 2021 de:

MANOVA y MANCOVA