Actualizado por ultima vez el 13 de septiembre de 2021, por Luis Benites.
Distribución Bimodal: Dos Picos.
Las distribuciones de datos en las estadísticas pueden tener un pico o pueden tener varios picos . El tipo de distribución con el que puede estar familiarizado es la distribución normal , o curva de campana , que tiene un pico. La distribución bimodal tiene dos picos.
Mire el video para obtener una descripción general de la distribución bimodal:
Distribución bimodal Mira este video en YouTube .
¿No puedes ver el vídeo? Haga clic aquí
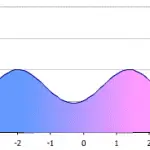
Distribución bimodal que muestra dos curvas de distribución normal combinadas, para mostrar picos. Crédito de la imagen: Maksim|Wikimedia Commons
El «bi» en la distribución bimodal se refiere a «dos» y modal se refiere a los picos. Puede parecer un poco confuso porque en estadística, el término “moda” se refiere al número más común. Sin embargo, si lo piensa, los picos en cualquier distribución son los números más comunes. Los dos picos en una distribución bimodal también representan dos máximos locales ; estos son puntos donde los puntos de datos dejan de aumentar y comienzan a disminuir.
P. ¿Qué le dice una distribución bimodal?
Tiene dos picos de datos, lo que generalmente indica que tiene dos grupos diferentes. Por ejemplo, las calificaciones de los exámenes tienden a tener una distribución normal con un solo pico. Sin embargo, las calificaciones a veces caen en una distribución bimodal con muchos estudiantes obteniendo calificaciones A y muchos obteniendo calificaciones F. Esto puede indicarle que está viendo dos grupos diferentes de estudiantes. Puede ser que un grupo no esté preparado para la clase (quizás debido a la falta de clases anteriores). El otro grupo puede haberse preparado en exceso.
Dos picos también podrían indicar que sus datos son sinusoidales . Si sospecha que sus datos podrían estar siguiendo un patrón similar a una onda, cree un diagrama de dispersión o un diagrama de secuencia de ejecución para verificar dos veces los patrones sinusoidales. También podría hacer un gráfico de retardo; un patrón elíptico confirmaría que los datos son sinusoidales.
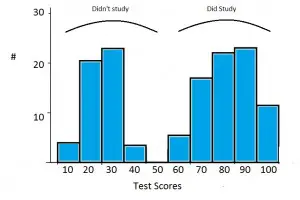
A veces, lo que parece ser una distribución bimodal son en realidad dos distribuciones unimodales (un pico) graficadas en el mismo eje. Por ejemplo, esta imagen muestra una distribución bimodal para un grupo de estudiantes que no estudiaron (el pico izquierdo) y un grupo de estudiantes que sí estudiaron (a la derecha).
Distribuciones Unimodales.
Las distribuciones unimodales tienen un solo pico o moda.
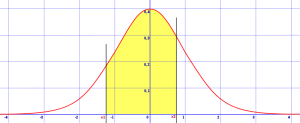
La distribución normal ( curva de campana ) es unimodal.
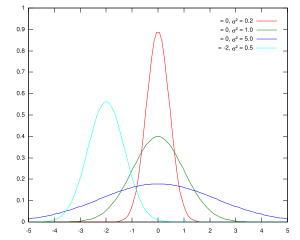
Varias distribuciones unimodales mostradas en el mismo gráfico. Crédito de la imagen: Grendelkhan|Wikimedia commons.
Distribuciones Multimodales
Las distribuciones multimidales tienen más de dos picos. Si no puede encontrar claramente uno o dos picos en un gráfico, lo más probable es que tenga una distribución uniforme (donde todos los picos tienen la misma altura) o una distribución multimodal, donde hay varios picos de la misma altura. . Sugerencia: aunque comúnmente podría asociar » modo

Además de ser el número que ocurre con mayor frecuencia en un conjunto de datos, el término moda en realidad tiene dos significados en las estadísticas, lo que puede resultar confuso: puede ser un máximo local en un gráfico o puede ser la puntuación que ocurre con mayor frecuencia en un gráfico. El «modo» en la distribución bimodal significa un máximo local en un gráfico (es decir, un modo local). Los dos términos en realidad significan lo mismo, ya que el elemento más comúnmente encontrado en un conjunto de datos tendrá un pico. Pero cuando intenta categorizar gráficos, es más fácil pensar en la moda como un «pico» en lugar de un número común. Esto ayuda especialmente si los ejes no están etiquetados.
Dato curioso: si bien la curva de campana normalmente se asocia con calificaciones (es decir, el 5 % de la clase obtendrá una A y el 10 % de la clase obtendrá una B), también es bastante normal tener una distribución bimodal en la que aproximadamente la mitad de una clase lo hará muy bien (obteniendo A y B) y la otra mitad de la clase recibirá malas calificaciones (D y F). ¡Las distribuciones bimodales son muy comunes en las clases de matemáticas de primer año de la universidad!
Referencias
Gonick, L. (1993). La guía de dibujos animados de estadísticas . Harper Perennial.
Kotz, S.; et al., editores. (2006), Enciclopedia de Ciencias Estadísticas , Wiley.
Everitt, BS; Skrondal, A. (2010), The Cambridge Dictionary of Statistics , Cambridge University Press.

