Actualizado por ultima vez el 2 de septiembre de 2021, por Luis Benites.
¿Qué es el procedimiento de Benjamini-Hochberg?
El Procedimiento Benjamini-Hochberg es una poderosa herramienta que disminuye la tasa de descubrimiento falso .
Ajustar la tasa ayuda a controlar el hecho de que, a veces , los valores p pequeños (menos del 5 %) ocurren por casualidad, lo que podría llevarlo a rechazar incorrectamente las hipótesis nulas verdaderas . En otras palabras, el Procedimiento BH te ayuda a evitar errores Tipo I (falsos positivos).
Un valor p del 5 % significa que solo hay un 5 % de posibilidades de que obtenga el resultado observado si la hipótesis nula fuera cierta. En otras palabras, si obtiene un valor p del 5%, es muy poco probable que su hipótesis nula no sea cierta y deba descartarse. Pero es solo una probabilidad: muchas veces, las verdaderas hipótesis nulas se descartan solo por la aleatoriedad de los resultados.
Un ejemplo concreto: Digamos que tienes un grupo de 100 pacientes que sabes que están libres de cierta enfermedad. Su hipótesis nula es que los pacientes están libres de la enfermedad y su alternativa es que sí tienen la enfermedad. Si ejecutó 100 pruebas estadísticas al 5 % de nivel alfa , aproximadamente el 5 % de los resultados se reportarían como falsos positivos.
No hay mucho que pueda hacer para evitar esto: cuando ejecuta pruebas estadísticas, una fracción siempre serán falsos positivos. Sin embargo, ejecutar el procedimiento BH disminuirá el número de falsos positivos.
Cómo ejecutar el procedimiento Benjamini-Hochberg
- Ponga los valores p individuales en orden ascendente.
- Asigne rangos a los valores p. Por ejemplo, el más pequeño tiene un rango de 1, el segundo más pequeño tiene un rango de 2.
- Calcule el valor crítico Benjamini-Hochberg de cada valor p individual, usando la fórmula (i/m)Q, donde:
- i = el rango del valor p individual,
- m = número total de pruebas,
- Q = la tasa de descubrimiento falso (un porcentaje, elegido por usted).
- Compare sus valores p originales con el BH crítico del Paso 3; encuentre el valor p más grande que sea más pequeño que el valor crítico.
Como ejemplo, la siguiente lista de datos muestra una lista parcial de resultados de 25 pruebas con sus valores p en la columna 2. La lista de valores p se ordenó (Paso 1) y luego se clasificó (Paso 2) en la columna 3. La columna 4 muestra el cálculo del valor crítico con una tasa de descubrimiento falso del 25% (Paso 3). Por ejemplo, la columna 4 para el elemento 1 se calcula como (1/25) * 0,25 = 0,01: el valor p en negrita (para niños) es el valor p más alto que también es más pequeño que el valor crítico: 0,042 < . 050. Todos
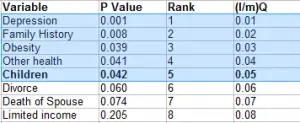
los valores por encima de él (es decir, aquellos con valores de p más bajos) se resaltan y se consideran significativos, incluso si esos valores de p son más bajos que los valores críticos. Por ejemplo, Obesidad y Otra salud no son significativos individualmente cuando compara el resultado con la columna final (p. ej., 0,039 > 0,03). Sin embargo, con la corrección BH, se consideran significativos; en otras palabras, rechazaría la hipótesis nula para esos valores.
Referencias
Beyer, WH CRC Standard Mathematical Tables, 31ª ed. Boca Raton, FL: CRC Press, págs. 536 y 571, 2002.
Agresti A. (1990) Análisis de datos categóricos. John Wiley and Sons, Nueva York.
Kotz, S.; et al., editores. (2006), Enciclopedia de Ciencias Estadísticas , Wiley.
Vogt, WP (2005). Diccionario de estadística y metodología: una guía no técnica para las ciencias sociales . SABIO.

