Prueba de Scheffe: definición, ejemplos, cálculo (paso a paso)

Actualizado por ultima vez el 18 de octubre de 2022, por Luis Benites.

¿Qué es el Test de Scheffe?

La prueba de Scheffe (también llamada procedimiento de Scheffe o método de Scheffe) es una prueba post-hoc utilizada en el análisis de varianza . Lleva el nombre del estadístico estadounidense Henry Scheffe . Después de ejecutar ANOVA y obtener una estadística F significativa (es decir, si ha rechazado la hipótesis nula de que las medias son las mismas), ejecute la prueba de Sheffe para averiguar qué pares de medias son significativos. La prueba de Scheffe corrige alfa para comparaciones de medias simples y complejas. Las comparaciones de medias complejas implican comparar más de un par de medias simultáneamente.

De las tres pruebas de comparación de medias que puede ejecutar (las otras dos son LSD de Fisher y HSD de Tukey ). La prueba de Scheffe es la más flexible, pero también es la prueba con menor poder estadístico . Decidir qué prueba ejecutar depende en gran medida de las comparaciones que le interesen:

• Si sólo desea realizar comparaciones por pares , ejecute el procedimiento de Tukey porque tendrá un intervalo de confianza más estrecho .
• Si desea comparar todos los posibles pares de medias simples y complejas, ejecute la prueba de Scheffe, ya que tendrá un intervalo de confianza más estrecho.

Cálculo de la prueba

Ejecute esta prueba solo si ha rechazado la hipótesis nula en una prueba ANOVA, lo que indica que las medias no son las mismas. De lo contrario, las medias son iguales, por lo que no tiene sentido ejecutar esta prueba.

• La hipótesis nula de la prueba es que todas las medias son iguales: H ₀ : μ _i = μ _j .
• La hipótesis alternativa es que las medias no son las mismas: H ₀ : μ _i ≠ μ _j .

Esta prueba generalmente se calcula con software. Como la mayoría de las pruebas estadísticas, encuentra un valor crítico y luego lo compara con una estadística de prueba. Rechazar la hipótesis nula si el estadístico de la prueba de Scheffe es mayor que el valor crítico.

Los pasos que siguen son para calcular comparaciones simples por pares a mano para cuatro muestras ABC y D. Necesitará datos estadísticos descriptivos (las medias de la muestra ) más datos de ANOVA (como el error cuadrático medio ).

Muestra Medias para Muestras ABCD:

• A = 36,00,
• B = 34,50,
• C = 35,60,
• D = 36,21.

Datos de ANOVA (de la salida de ANOVA)

• Valor F = 3,24 (de la tabla f , con 3 grados de libertad en el numerador y 16 grados de libertad en el denominador con un α de 0,05).
• Error cuadrático medio: 0,028.

Pasos

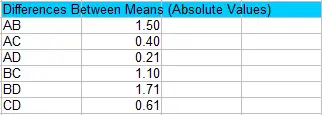
Paso 1: Calcular los valores absolutos de las diferencias por pares entre las medias de las muestras. Tendrás que averiguar todas las combinaciones posibles . Para cuatro muestras, hay 6 combinaciones posibles de dos: AB AC AD BC BD y CD.
Por ejemplo, para AB la diferencia absoluta (|AB|) es 36,00 – 34,50 = 1,50.

Paso 2: use la siguiente fórmula para encontrar un conjunto de valores de la fórmula de Scheffe (los usará en el próximo paso): Donde:

• (k – 1) es el grado de libertad entre muestras . Para este conjunto de datos, eso es 3 (4 – 1 = 3).
• F , 1 * norte – kk – ; α = el valor f (de ANOVA) . Para este conjunto de datos, el valor f es 3,24.
• MSE = error cuadrático medio (de ANOVA) .

¡Es más fácil de lo que parece! Una vez que haya encontrado el df y el MSE de su salida de ANOVA, solo necesita cambiar los tamaños de muestra en la fórmula para cada comparación. (Los tamaños de muestra son A = 5, B = 6, C = 4, D = 5).
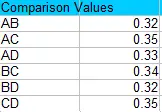
Por ejemplo, comparando A y B obtenemos:
√(3 * 3,24 * 0,028 *( 1/5 + 1/6 )) = 0,32.
Y comparando A y C obtenemos:
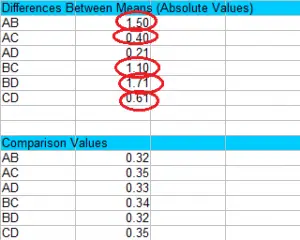
√(3 * 3,24 * 0,028 *( 1/5 + 1/4 )) = 0,35. Paso 3: Compare los valores del Paso 1 con los valores del Paso 2 y encuentre cualquier valor que sea mayor que los valores de comparación. Los valores más grandes son estadísticamente significativos en el nivel alfa elegido (en este caso, 0,05). Para este ejemplo, el único valor que no es significativo es AD, porque 0,21 es menor que 0,33. ¡Eso es todo! 

Referencias

Henry Scheffe. (1999). El análisis de varianza . John Wiley & Sons.