Actualizado por ultima vez el 30 de enero de 2022, por Luis Benites.
¿Qué es Pairwise?
En pares significa formar todos los pares posibles , dos elementos a la vez, de un conjunto. Por ejemplo, en el conjunto {1,2,3} todos los pares posibles son (1,2),(2,3),(1,3).
Promedios por parejas (promedios de Walsh)
Los promedios por pares (Walsh) son promedios calculados a partir de cada par en un conjunto, incluido un par emparejado consigo mismo. Por ejemplo, el conjunto {2,9} tiene tres pares: (2,2),(9,9) y (2,9). Los promedios de Walsh para este conjunto son:
- (2,2) = 2
- (9,9) = 9
- (2,9) = 5,5.
Después de esto, los promedios de Walsh se utilizan en pruebas como Signed-Rank Wilcoxon y otras pruebas no paramétricas . En las pruebas de rango con signo de Wilcoxon, la estadística de prueba es igual al número de promedios de Walsh positivos (llamados «compensaciones»). La fórmula formal es: (D 1 – D 2 )/2, donde D es un punto de datos.
Comparación por pares
La comparación por pares es el acto de formar pares con el objetivo de compararlos de alguna manera. Se utiliza para comparaciones directas. Cada candidato se enfrenta a todos los demás candidatos y se otorgan puntos por una «victoria». La persona/elemento con más premios se declara ganador.
Ejemplo : Digamos que Washington, Garfield, LBJ y Kennedy se presentaron a las elecciones hoy. Los resultados se cuentan para los primeros 4 estados que informan: para saber quién está a la cabeza, necesitamos saber quién ganó la mayoría de los enfrentamientos. Hay varias maneras de hacer esto. Tal vez la más fácil sea una tabla de doble entrada . He bloqueado cuadrados duplicados (por ejemplo, Washington/Garfield está en un cuadrado mientras que Garfield/Washington está en otro) y cualquier cuadrado donde una persona se enfrente a sí misma (por ejemplo, Washington/Washington): A continuación, complete los ganadores de cada cabeza a la cabeza Estoy asignando 4 puntos para el 1er lugar, 3 puntos para el 2do lugar, 2 puntos para el 3er lugar y 1 punto para el cuarto lugar.
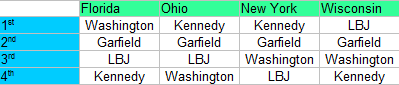

- Washington: 4 + 1 + 2 + 2 = 9 puntos.
- Garfield: 3 + 3 + 3 + 3 = 12 puntos.
- LBJ: 2 + 2 + 1 + 4 = 9 puntos.
- Kennedy: 1 + 4 + 4 + 1 = 10 puntos.
Cada pareja se empareja cara a cara. Por ejemplo, Garfield (con 12 puntos) gana a Washington (9 puntos) y Garfield/LBJ está empatado: con solo mirar los resultados podemos ver que Garfield tiene la mayor cantidad de «victorias».

Si la respuesta no es obvia, otorgue 1 punto por victoria y 1/2 punto por empate. Los resultados de este enfrentamiento serían:
- Washington: 1/2 punto
- Garfield: 3 puntos
- LBJ: 1.2 punto
- Kennedy: 2 puntos
Diferencias por pares
Para encontrar diferencias por pares para dos columnas de igual longitud:
- Empareje cada valor en una columna con cada valor en una segunda columna.
- Calcula las diferencias.
Ejemplo :

- Empareje cada valor de la columna A con cada valor de la columna B: (3,7), (3,2), (3,10), (4,7), (4,2), (4,10), ( 5,7), (5,2), (5,10).
- Calcula las diferencias entre cada par. Por ejemplo, la diferencia para el primer par es 3 – 7 = -4, el segundo par es 3 – 2 = 1 y el tercer par es 3 – 10 = -7. En total, tendrás un total de 9 diferencias para este conjunto.
Pendientes por pares
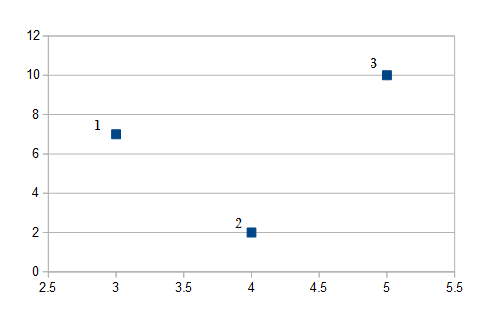
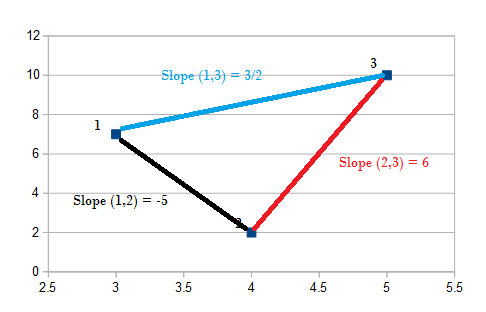
Las pendientes por pares también se calculan para columnas de datos, excepto que cada columna representa valores X e Y. Las pendientes se calculan para cada par. Por ejemplo, supongamos que tiene las siguientes dos columnas de datos: Un diagrama de dispersión de los datos se vería así: Para comenzar, simplemente use la fórmula de la pendiente (del álgebra elemental) para encontrar las pendientes de cada par. Para este ejemplo hay tres pares (1,2), (1,3), (2,3), por lo que usando la fórmula de la pendiente (y 2 – y 1 ) / (x 2 – x 1 ): 1ro. Pendiente (1,2) = (2-7)/(4-3) = -5/1 = -5 2do. Pendiente (1,3) = (10-7)/(5-3) = 3/2 3er. Pendiente (2,3) = (10-4)/(5-4) = 6/1 = 6

Pares Independientes / Mutuamente Independientes
¿Qué es «independiente por pares»?
Independiente por pares significa que cada evento es independiente de cualquier otra combinación posible de eventos emparejados. En otras palabras, la probabilidad de un evento en cada par posible (por ejemplo, AB AC BC) no tiene relación con la probabilidad del otro evento en el par.
¿Qué es Mutuamente Independiente?
Los eventos A, B y C son mutuamente independientes si son independientes por pares:
P(A ∩ B) = P(A) × P(B) y…
P(A ∩ C) = P(A) × P(C) y…
P(B ∩ C) = P(B) × P(C)
Y :
P(A ∩ B ∩ C) = P(A) × P(B) × P(C), lo que indica que sus probabilidades , cuando se multiplica, es también la probabilidad de la intersección de los tres eventos.
Por definición, los eventos mutuamente independientes también son independientes por pares. Pero un conjunto de eventos que es independiente por pares no es automáticamente independiente entre sí. También deben cumplir la condición P(A ∩ B ∩ C) = P(A) × P(B) × P(C).
Problema de ejemplo
Pregunta: Lanzas una moneda justa dos veces. Los eventos posibles son:
- Ambos lanzamientos dan el mismo resultado (HH o TT).
- El primer lanzamiento es cara (HT HH).
- El segundo lanzamiento es cara (TH HH).
¿Son los eventos mutuamente independientes?
Respuesta:
Lo que la pregunta realmente es: ¿estos eventos se ajustan a la definición establecida anteriormente (justo debajo de ¿Qué es mutuamente independiente?). La definición establece que lo siguiente debe ser cierto:
P (A ∩ B ∩ C) = P (A) × P(B) × P(C),
Entonces, primero debemos calcular algunas probabilidades a partir de la información dada.
P(evento 1), P(evento 2) y P(3).
Tiene cuatro resultados posibles (HH, TT, TH, HT), por lo que la probabilidad de que ocurra cada par es 0,25. Esto haría que las probabilidades de los eventos 1, 2 y 3:
- Ambos lanzamientos dan el mismo resultado (HH o TT) = 1/4 + 1/4 = 1/2.
- El primer lanzamiento es cara (HT HH) = 1/4 + 1/4 = 1/2..
- El segundo lanzamiento es cara (TH HH) = 1/4 + 1/4 = 1/2..
Multiplica la probabilidad de eventos juntos:
P(1) * P(2) * P(3) = 1/2 * 1/2 * 1/2 = 1/8.
P(1 ∩ 2) = P(1 ∩ 3) = P(2 ∩ 3) = 1/4.
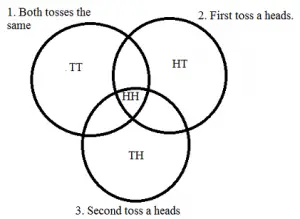
Esto se debe a que HH es el único evento que se cruza (una probabilidad de 1 de 4). Si tiene problemas para descifrar las intersecciones, un diagrama de Venn siempre es una buena idea. el siguiente diagrama te ayudará a ver que HH es la intersección de las tres probabilidades: Esto también nos da P(1 ∩ 2 ∩ 3 ∩) = 1/4.
Ahora puedes comparar los dos:
P(1 ∩ 2 ∩ 3) = P(1) × P(2) × P(3)
1/8 ≠ 1/4
Estos no son iguales, por lo que los eventos no son mutuamente independientes.
Estadísticas por pares
Estas son estadísticas calculadas a partir de pares de observaciones. En otras palabras, forma pares de observaciones y luego encuentra una estadística de interés, como una media o una desviación estándar .
Referencias :
Rosenbaum, P. Intervalos de confianza exactos para efectos no constantes mediante la inversión de la prueba de rango con signo. The American Statistician, mayo de 2003, vol. 57, No. 2 Recuperado el 8 de octubre de 2016 de aquí . URL: http://stat.wharton.upenn.edu/~rosenbap/offsetEdit.pdf

