Intervalo Z: definición simple, fórmula y ejemplo resuelto

Actualizado el 23 de marzo de 2022, por Luis Benites.

«Intervalo Z» podría referirse a:

1. Un tipo específico de intervalo de confianza (ver más abajo), o
2. Una opción de calculadora TI-83 para encontrar un intervalo de confianza para la media utilizando el intervalo Z. Si está utilizando la TI-83, consulte este artículo sobre intervalos de confianza para obtener instrucciones paso a paso sobre el intervalo Z de la TI-83.

Es posible que desee leer este artículo primero: ¿Qué es un intervalo de confianza?

¿Qué es un intervalo Z?

Un intervalo z es un tipo específico de intervalo de confianza que le indica un rango en el que puede esperar que caiga una media o proporción particular. Se puede calcular a partir de una desviación estándar conocida .

Intervalo Z frente a intervalo T

En general, desea elegir calcular intervalos z cuando:

• El tamaño de su muestra es 30 o más,
• Conoces la desviación estándar de tu muestra .

Cuando no conoce la desviación estándar y aún desea encontrar un intervalo de confianza, calcule un intervalo t en su lugar. El concepto es el mismo, excepto que usa una tabla diferente para calcular el intervalo: la tabla z para un intervalo z y una tabla t para un intervalo t. Para obtener más información sobre las diferencias específicas entre «T» y «Z», consulte: Puntajes T frente a puntajes Z.

Cómo calcular el intervalo Z

¿ Necesita ayuda con una pregunta de tarea? ¡Mira nuestra página de tutoría!

Un intervalo z para una media viene dado por la fórmula: La fórmula puede parecer un poco desalentadora, pero las partes individuales son bastante fáciles de encontrar:

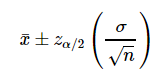
• n es el tamaño de la muestra.
• σ es la desviación estándar.
• x̄ es la media muestral
• z _α/2 es la puntuación z de un nivel alfa para una prueba de dos colas (consulte la nota a continuación).

Nota : si z _α/2 es nuevo para usted, lea todo sobre z _α/2 aquí . La mayoría de las veces, no tendrás que hacer ningún cálculo porque los valores más comunes ya se conocen:

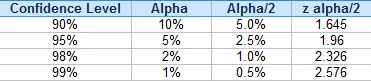
Para la mayoría de las pruebas estadísticas, probablemente utilizará uno de los cuatro intervalos de confianza (90 %, 95 %, 98 % y 99 %). El z alfa/2 para cada nivel de confianza es siempre el mismo:

Por ejemplo, si está tratando de encontrar un intervalo z con un nivel de confianza del 90 % y un nivel alfa (de significación) del 5 %, utilice 1,645 en la ecuación anterior.

Ejemplo

Supongamos que queremos calcular un intervalo de confianza del 95 por ciento para una situación en la que sabemos:

• Media (μ) = 50,
• Desviación estándar = 5,
• El número de puntos de datos en la muestra es 81.

Para un intervalo de confianza del 95 %, la tabla anterior nos dice que z _0.025 = 1.96.

Ahora tenemos todos los datos para incluir en nuestra fórmula y nuestro intervalo de confianza será:

Podemos simplificar esto a:

que es nuestro intervalo de confianza o intervalo z.

Referencias

Gonick, L. (1993). La guía de dibujos animados de estadísticas . Harper Perennial.
Everitt, BS; Skrondal, A. (2010), The Cambridge Dictionary of Statistics , Cambridge University Press.
Kotz, S.; et al., editores. (2006), Enciclopedia de Ciencias Estadísticas , Wiley.
Programas en línea del Departamento de Estadística de la Universidad Estatal de Pensilvania. STAT 414 Introducción a la Teoría de la Probabilidad. Lección 30 Intervalos de confianza para una media. Recuperado de https://newonlinecourses.science.psu.edu/stat414/node/194/ y https://newonlinecourses.science.psu.edu/stat414/node/196/ el 30 de mayo de 2018.
Walker, Jerimi Ann. Intervalos de confianza para la media a mano. Obtenido de
https://www.mathbootcamps.com/calculating-confidence-intervals-for-the-mean/ el 30 de mayo de 2018.Xie, Yao. Apuntes de clase: Intervalo de confianza. Recuperado de https://www2.isye.gatech.edu/~yxie77/isye2028/lecture7.pdf el 30 de mayo de 2018.