¿Cómo normalizar datos entre 0 y 1?

Actualizado el 2 de abril de 2022, por Dereck Amesquita.

Para normalizar los valores de un conjunto de datos entre 0 y 1, puede utilizar la siguiente fórmula:

z _i = (x _i – mínimo (x)) / (máximo (x) – mínimo (x))

dónde:

• z _i : El i- ^ésimo valor normalizado en el conjunto de datos.
• x _i : el i- ^ésimo valor en el conjunto de datos.
• min (x) : el valor mínimo en el conjunto de datos.
• max (x): el valor máximo en el conjunto de datos.

Si no entiendes esta formula, no te preocupes, pues comenzaremos con un ejemplo y si aun a pesar de ello tuvieses dudas te explicare la lógica detrás.

Ejemplo de Normalización de Datos

Por ejemplo, supongamos que tenemos el siguiente conjunto de datos:

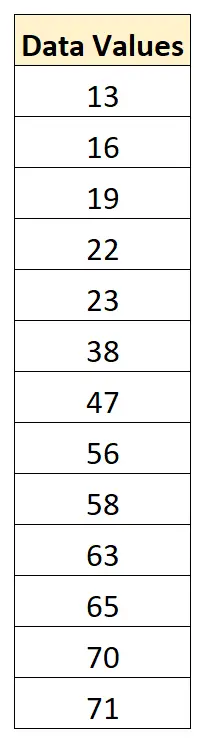
El valor mínimo en el conjunto de datos es 13 y el valor máximo es 71.

Para normalizar el primer valor de 13 , aplicaríamos la fórmula compartida anteriormente:

• z _i = (x _i  – mínimo (x)) / (máximo (x) – mínimo (x)) = (13 – 13) / (71 – 13) = 0

Para normalizar el segundo valor de 16 , usaríamos la misma fórmula:

• z _i = (x _i – mínimo (x)) / (máximo (x) – mínimo (x)) = (16 – 13) / (71 – 13) = .0517

Para normalizar el tercer valor de 19 , usaríamos la misma fórmula:

• z _i = (x _i  – mínimo (x)) / (máximo (x) – mínimo (x)) = (19 – 13) / (71 – 13) = .1034

Podemos usar esta misma fórmula exacta para normalizar cada valor en el conjunto de datos original entre 0 y 1:

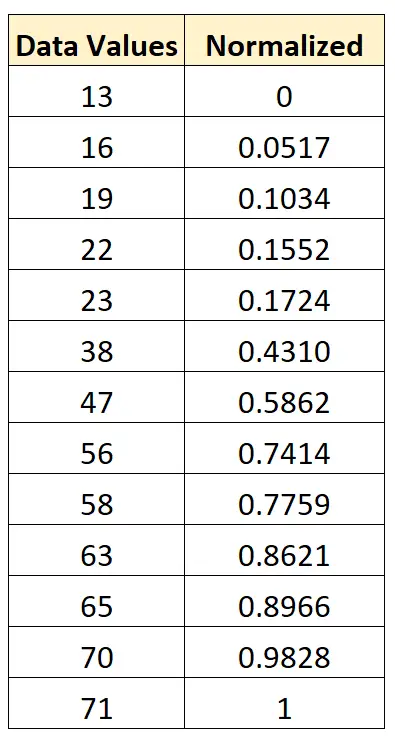
Con este método de normalización, las siguientes afirmaciones siempre serán verdaderas:

• El valor normalizado para el valor mínimo en el conjunto de datos siempre será 0.
• El valor normalizado para el valor máximo en el conjunto de datos siempre será 1.
• Los valores normalizados para todos los demás valores del conjunto de datos estarán entre 0 y 1.

La lógica detrás de la normalización de datos

Regresemos a la función básica:

• z _i = (x _i  – mínimo (x)) / (máximo (x) – mínimo (x))

Ahora supongamos que nuestros números a normalizar van en una escala del 0 al 1. Es decir, ya están normalizados. Ahora nuestro máximo es 1 y nuestro mínimo es 0. Por lo cual el denominador «(máximo (x) – mínimo (x))» seria 1-0 = 1, todo numero dividido por 1 es igual al mismo. Es decir no cambiaria, lo que sucede es que en el denominador buscamos la distancia, si decimos que el punto a se encuentra en la cuadra 3 y el punto b se encuentra en la cuadra 8, tendríamos que restar el máximo con el mínimo, obteniendo la distancia la cual es 5. Por esta razón, si el punto a avanza a la cuadra 6, tendremos que restarle el mínimo para saber en realidad cuanto avanzo (6-3 igual a 3), es decir avanzo 3 cuadras, y eso lo obtenemos en el numerador. Al final obtenemos 3/5 lo que es 0.60, obtenemos un valor en la escala de 0 y 1, el cual es la proporción de lo que se avanzo.

¿Cuándo normalizar los datos?

A menudo normalizamos variables al realizar algún tipo de análisis en el que tenemos múltiples variables que se miden en diferentes escalas y queremos que cada una de las variables tenga el mismo rango.

Esto evita que una variable sea demasiado influyente, especialmente si se mide en diferentes unidades (es decir, si una variable se mide en pulgadas y otra en yardas).

También vale la pena señalar que usamos un método conocido como normalización mínima-máxima en este tutorial para normalizar los valores de los datos.

Los dos métodos de normalización más comunes son los siguientes:

1. Normalización Min-Max

• Objetivo: convierte cada valor de datos en un valor entre 0 y 100.
• Fórmula: Nuevo valor = (valor – min) / (max – min) * 100

2. Normalización media

• Objetivo: Escala los valores de manera que la media de todos los valores sea 0 y std. dev. es 1.
• Fórmula: Nuevo valor = (valor – media) / (desviación estándar)

Recursos adicionales

Los siguientes tutoriales explican cómo normalizar datos utilizando diferentes softwares estadísticos:

Cómo normalizar datos en Excel
Cómo normalizar datos en R
Cómo normalizar columnas en Python

• https://r-project.org
• https://www.python.org/
• https://www.stata.com/