Contenido de este artículo
- 0
- 0
- 0
- 0
Actualizado el 21 de agosto de 2021, por Luis Benites.
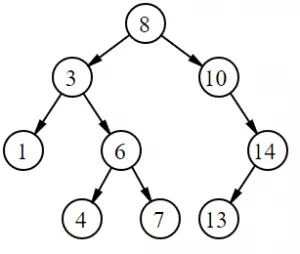Los árboles binarios son gráficos o estructuras de datos de árbol donde cada nodo (que se muestra como círculos en el gráfico de la izquierda) tiene hasta dos posibles ramas («hijos»). Estos se llaman la rama izquierda y la rama derecha o, a veces, el hijo izquierdo y el hijo derecho.
Aunque son estructuras relativamente simples, los árboles binarios son extremadamente útiles para modelar datos. Por ejemplo, los números racionales se pueden representar con una variante del árbol binario, llamada árbol de Calkin-Wilf . También se pueden utilizar para representar jerarquías y reflejar relaciones estructurales en los datos. Son flexibles; podemos mover ‘subárboles’ fácilmente dentro de un árbol según sea necesario. También se pueden buscar y analizar de manera muy eficiente por computadora.
Definiciones importantes para árboles binarios
El nodo superior de un árbol (8 en la imagen de arriba) se llama nodo raíz .
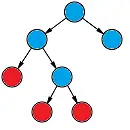
Árbol binario que muestra los nodos internos (azul) y los nodos externos (rojo).
Un nodo externo es uno sin ramas secundarias, mientras que un nodo interno tiene al menos una rama secundaria.
El tamaño de un árbol binario se refiere a la cantidad de nodos que tiene.
La distancia desde un nodo B hasta el nodo raíz es el nivel de B. La raíz está en el nivel 0, los hijos de la raíz están en el nivel 1, y así sucesivamente.
La suma de los niveles de cada uno de los nodos internos de un árbol se denomina longitud de ruta interna de ese árbol.
La suma de los niveles de cada uno de los nodos externos en un árbol se denomina longitud del camino externo .
El nivel máximo, entre todos los nodos externos, se denomina altura del árbol .
Más terminología de árboles binarios
Un árbol que tiene un nodo raíz se llama árbol enraizado. Si cada nodo tiene como máximo dos ramas, se convierte en un árbol binario y es un árbol binario enraizado .
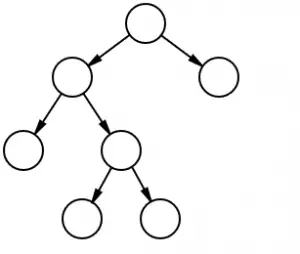
Un árbol binario completo
Un árbol donde cada nodo (excepto las hojas) tiene 2 ramas se llama árbol binario completo . Los árboles binarios completos a veces también se denominan árboles binarios propios o planos.
Un árbol en el que todos los nodos interiores tienen dos ramas y todos los nodos con 0 ramas (nodos hoja) están al mismo nivel o tienen la misma profundidad se denomina árbol binario perfecto .
Un árbol binario que está completamente lleno, excepto potencialmente el nivel inferior, que se llena de izquierda a derecha, se denomina árbol binario completo . Los árboles binarios completos son importantes porque proporcionan la mejor relación entre la altura de un árbol y el número de nodos.
Referencias
Sedgewick y Flajolet. Una introducción al análisis de algoritmos. Recuperado el 24 de noviembre de 2017 de:
recuperado de http://aofa.cs.princeton.edu/60trees/.
Parlante, N. Árboles binarios. Recuperado el 24 de noviembre de 2017 de:
recuperado de http://cslibrary.stanford.edu/110/BinaryTrees.html
Redactor del artículo
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo:
