Actualizado por ultima vez el 21 de mayo de 2022, por Luis Benites.
Puede que le resulte útil leer primero el precioso artículo: ¿Qué es el tamaño del efecto?
¿Qué es la D de Cohen?
La D de Cohen , o diferencia de medias estandarizada , es una de las formas más comunes de medir el tamaño del efecto. El tamaño del efecto es qué tan grande es un efecto. Por ejemplo, el medicamento A tiene un efecto mayor que el medicamento B. Mientras que un valor de p puede decirle si hay un efecto, no le dirá qué tan grande es ese efecto.
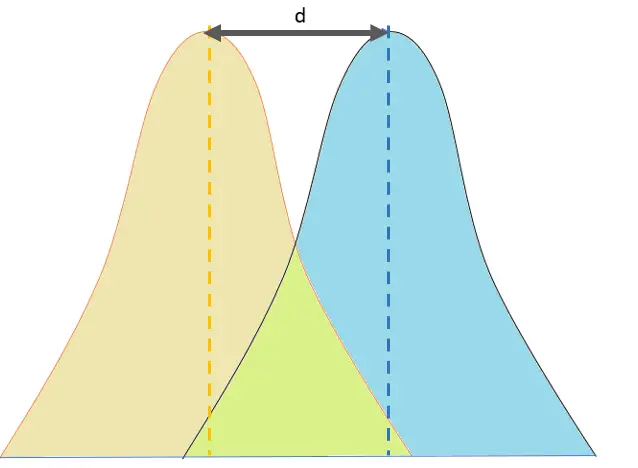
La D de Cohen mide específicamente el tamaño del efecto de la diferencia entre dos medias.
Mire el video para ver un ejemplo de cómo calcular la D de Cohen (incluye fórmulas para corrección de muestras pequeñas y tamaños desiguales):
D de Cohen 
Mira este video en YouTube .
¿No puedes ver el vídeo? Haga clic aquí
Fórmula
La fórmula para la D de Cohen (para grupos de igual tamaño) es:
d = (M 1 – M 2 ) / s agrupados
Donde:
- M 1 = media del grupo 1
- M 2 = media del grupo 2
- s combinado = desviaciones estándar combinadas para los dos grupos. La fórmula es: √[(s 1 2 + s 2 2 ) / 2]
La D de Cohen funciona mejor para tamaños de muestra más grandes (> 50). Para tamaños de muestra más pequeños, tiende a inflar demasiado los resultados. Hay disponible un factor de corrección que reduce el tamaño del efecto para muestras pequeñas en unos pocos puntos porcentuales: Nota : el sesgo hacia el sesgo de muestras pequeñas es ligeramente menor para un método alternativo, Hedges’ g , que usa n-1 para cada muestra.
Interpretación de resultados
Una d de 1 indica que los dos grupos difieren en 1 desviación estándar , una d de 2 indica que difieren en 2 desviaciones estándar, y así sucesivamente. Las desviaciones estándar son equivalentes a las puntuaciones z (1 desviación estándar = 1 puntuación z).
Interpretación de la regla general
Si no está familiarizado con el significado de las desviaciones estándar y las puntuaciones z, o tiene problemas para visualizar el resultado de la D de Cohen, use estas pautas generales de «regla general » (que Cohen dijo que deben usarse con precaución):
- Efecto pequeño = 0,2
- Efecto Medio = 0.5
- Efecto grande = 0,8
Los efectos “pequeños” son difíciles de ver a simple vista. Por ejemplo, Cohen informó que la diferencia de altura entre las niñas de 15 y 16 años en los EE. UU. es aproximadamente de este tamaño del efecto. «Medio» es probablemente lo suficientemente grande como para ser discernido a simple vista, mientras que los efectos que son «grandes» definitivamente se pueden ver a simple vista (Cohen llama a esto «groseramente perceptible y, por lo tanto, grande»). Por ejemplo, la diferencia de altura entre las niñas de 13 y 18 años es de 0,8. Un efecto por debajo de 0,2 puede considerarse trivial, incluso si sus resultados son estadísticamente significativos .
Tenga en cuenta que un efecto «grande» no es necesariamente mejor que un efecto «pequeño», especialmente en entornos donde las pequeñas diferencias pueden tener un gran impacto . Por ejemplo, un aumento en las calificaciones académicas o de salud con un tamaño del efecto de solo 0,1 puede ser muy significativo en el mundo real. Durlak (2009) sugiere consultar investigaciones anteriores para tener una idea de dónde encajan sus hallazgos en el contexto más amplio.
Transformar la D de Cohen en otras medidas
Para transformar la D de Cohen en la g de Hedge, utilice la siguiente ecuación: Donde:
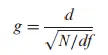
- N = tamaño de la muestra,
- gl = grados de libertad .
Para transformar la d de Cohen en el coeficiente de correlación , r, utilice esta fórmula:
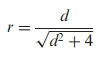
Referencias
Agresti A. (1990) Análisis de datos categóricos. John Wiley and Sons, Nueva York.
Klein, G. (2013). La caricatura Introducción a la estadística. Colina y Wamg.
Kotz, S.; et al., editores. (2006), Enciclopedia de Ciencias Estadísticas , Wiley.
Vogt, WP (2005). Diccionario de estadística y metodología: una guía no técnica para las ciencias sociales . SABIO.
