Contenido de este artículo
Actualizado el 4 de diciembre de 2021, por Luis Benites.
¿Qué es una desviación estándar agrupada?
La desviación estándar agrupada es un promedio ponderado de las desviaciones estándar de dos o más grupos. Las desviaciones estándar individuales se promedian, y se otorga más «peso» a los tamaños de muestra más grandes.
Mire el video para obtener una descripción general y un ejemplo de cálculo:
Desviación estándar agrupada Mira este video en YouTube .
¿No puedes ver el vídeo? Haga clic aquí.
Una vez que se ha calculado la desviación estándar agrupada, se usa SD agrupada en lugar de SD 1 y SD 2 en la fórmula para el error estándar . Junto con una fórmula actualizada de grados de libertad (df = n 1 + n 2 – 2), la idea es que podría obtener un mejor modelo para la distribución muestral de la media muestral .
Las desviaciones estándar agrupadas se utilizan en muchas áreas de las estadísticas, que incluyen: cálculos del tamaño del efecto , pruebas t y ANOVA . También se utilizan en ciencias de laboratorio como la biología y la química, donde pueden ser una indicación de la repetibilidad de un experimento.
Cómo calcular la desviación estándar agrupada
Cohen (1988) ofrece un par de opciones para calcular la desviación estándar agrupada. La más simple es: Donde :
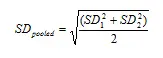
- SD 1 = desviación estándar para el grupo 1
- SD 2 = desviación estándar para el grupo 2
Incluyo la fórmula alternativa de Cohen aquí como referencia, aunque no hay un beneficio claro al usar esta en lugar de la fórmula más simple anterior: Donde :
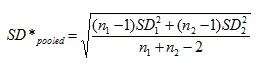
- x̄ = la media de la muestra
- n 1 = tamaño de la muestra para el grupo 1
- n 2 = tamaño de la muestra para el grupo 2
Para tres o más grupos , cambie el “2” en el denominador para reflejar el número de muestras, k: Para tamaños de muestra iguales , la fórmula se puede simplificar a:
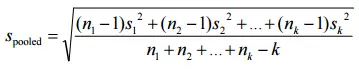
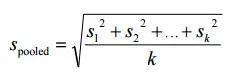
Solo puede usar las fórmulas anteriores si las desviaciones estándar para los dos grupos son las mismas (esto se debe a que, de lo contrario, estaría violando la suposición de homogeneidad de las varianzas ). Si las desviaciones estándar son diferentes, ejecute Hedge’s g o Glass’s Delta en su lugar.
Referencias
Gonick, L. (1993). La guía de dibujos animados de estadísticas . Harper Perennial.
Klein, G. (2013). La caricatura Introducción a la estadística. Colina y Wamg.
Kotz, S.; et al., editores. (2006), Enciclopedia de Ciencias Estadísticas , Wiley.
Lindström, D. (2010). Schaum’s Easy Outline of Statistics , segunda edición (Schaum’s Easy Outlines) 2ª edición. Educación McGraw-Hill
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo:
