Contenido de este artículo
Actualizado el 17 de julio de 2024, por Luis Benites.
La varianza y la covarianza son dos términos que se utilizan a menudo en estadística. Aunque suenan similares, son bastante diferentes.
La varianza mide la dispersión de los valores en un conjunto de datos determinado. Es decir una sola variable.
La covarianza mide cómo los cambios en una variable se asocian con los cambios en una segunda variable. Es decir dos variables.
Este tutorial proporciona una breve explicación de cada término junto con ejemplos de cómo calcular cada uno.
Fórmula de la varianza, ejemplo y cuándo utilizar
La varianza mide la dispersión de los valores en un conjunto de datos determinado.
La Fórmula de la Varianza:
La fórmula para encontrar la varianza de una muestra (denotada como s 2 ) es:
s 2 = Σ (x i – x ) 2 / (n-1)
dónde:
- x : la media de la muestra
- x i : La i- ésima observación en la muestra
- N : el tamaño de la muestra
- Σ : un símbolo griego que significa «suma»
Ejemplo del uso de la varianza:
Supongamos que tenemos el siguiente conjunto de datos con 10 valores:
Conjunto de datos: 6, 7, 10, 13, 14, 14, 18, 19, 22, 24
Usando una calculadora, podemos encontrar que la varianza muestral es 36.678 .
Ahora suponga que tenemos otro conjunto de datos con 10 valores:
Conjunto de datos: 6, 13, 19, 24, 25, 30, 36, 43, 49, 55
La varianza muestral de este conjunto de datos resulta ser 248,667 .
La varianza del segundo conjunto de datos es mucho mayor que la del primero, lo que indica que los valores del segundo conjunto de datos están mucho más dispersos en comparación con los valores del primer conjunto de datos.
Cuándo usar la varianza:
Usamos la varianza cuando queremos cuantificar qué tan dispersos están los valores en un conjunto de datos. Cuanto mayor sea la varianza, más dispersos serán los valores. El valor de la varianza puede oscilar entre cero (sin dispersión) y cualquier número mayor que cero.
Covarianza: definición, ejemplo y cuándo utilizar
La covarianza mide cómo los cambios en una variable se asocian con los cambios en una segunda variable.
Fórmula de la covarianza:
La fórmula para encontrar la covarianza entre dos variables, X e Y es:
COV ( X , Y ) = Σ (x i – x ) (y i – y ) / n
dónde:
- x : La media muestral de la variable X
- x i : La i- ésima observación de la variable X
- y : la media muestral de la variable Y
- y i : La i- ésima observación de la variable Y
- n : el número total de observaciones por pares
- Σ : un símbolo griego que significa «suma»
Ejemplo del uso de la covarianza:
Supongamos que tenemos el siguiente conjunto de datos con 10 valores:
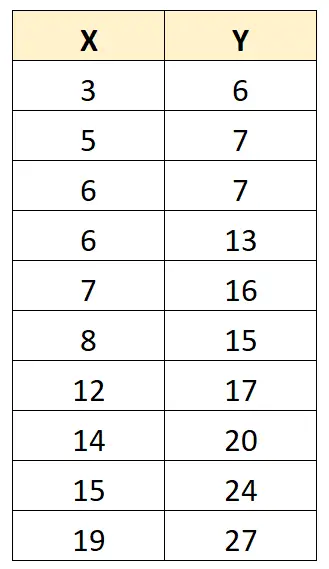
Usando una calculadora, podemos encontrar que la covarianza entre X e Y es 31,8 .
Dado que este valor es positivo, nos dice que a medida que aumentan los valores de X , los valores de Y tienden a aumentar también.
Ahora suponga que tenemos otro conjunto de datos con 10 valores:
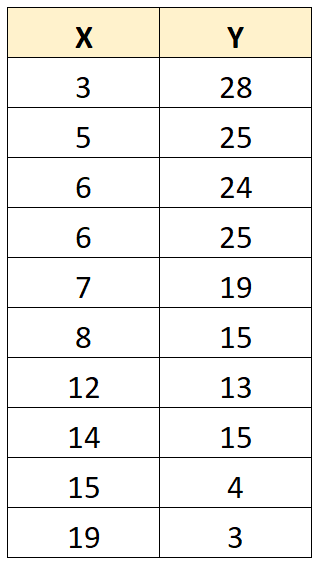
Usando una calculadora, podemos encontrar que la covarianza entre X e Y es -38.55 .
Dado que este valor es negativo, nos dice que a medida que aumentan los valores de X , los valores de Y tienden a disminuir.
Cuándo usar la covarianza:
Usamos la covarianza cuando queremos cuantificar la relación entre dos variables. Un valor positivo para la covarianza indica una relación positiva entre dos variables, mientras que un valor negativo indica una relación negativa entre dos variables.
Recursos adicionales
Medidas de dispersión: varianza, desviación estándar y calculadora de matriz de covarianza de rango intercuartílico
- https://r-project.org
- https://www.python.org/
- https://www.stata.com/
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo:
