Diferencia entre BinomPDF y BinomCDF; Pasos simples para ingresar datos

Actualizado el 25 de enero de 2022, por Luis Benites.

Diferencia entre BinomPDF y BinomCDF: descripción general

Mire el video para obtener una descripción general:

binompdf vs binomcdf en la calculadora TI Mira este video en YouTube .
¿No puedes ver el vídeo? Haga clic aquí

BinomPDF y BinomCDF son funciones para evaluar distribuciones binomiales en una calculadora gráfica TI . Ambos le darán probabilidades para distribuciones binomiales. La principal diferencia es que BinomCDF te da probabilidades acumulativas .

BinomPDF

BinomPDF es la probabilidad de que haya X éxitos en n intentos si hay una probabilidad p de éxito para cada intento. Por ejemplo, si n = 10, p = 0,5 y x = 3, BinomPDF devolverá 0,117. Eso significa que hay una probabilidad de .117 (11.7%) de que haya 3 éxitos.

Use BinomPDF cuando tenga preguntas que tengan:

• Un número exacto, como: todo, la mitad, ninguno o un número específico X.

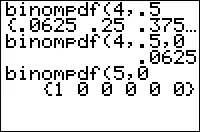
BinomCDF

Esta función es exactamente igual que BinomPDF, excepto que en lugar de un número específico de éxitos (es decir, «3 intentos»), esta función le da la probabilidad de que haya de 0 a x éxitos en n intentos. En otras palabras, si pones X=3 te dará la probabilidad de 0,1,2 y 3 intentos (todos juntos). Por ejemplo, si ingresa los mismos números que en el ejemplo anterior de BinomPDF (n = 10, p = .5, x = 3), obtendrá .172 (17.2 %) con BinomCDF. Este porcentaje es más alto ya que suma todas las probabilidades a X=3, de la misma manera que agrega probabilidades en una tabla de distribución de frecuencia acumulada .

Utilice BinomCDF cuando tenga preguntas con una redacción similar a:

• No más que, a lo sumo, no excede.
• Menos que o menos que.
• Al menos, más que, o más, no menos de X, no menos de X.
• Entre dos números (ejecutar BinomCDF dos veces).

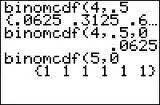
Calculadora BinomCDF TI 83: descripción general

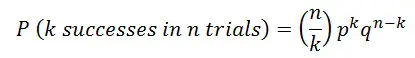
Las funciones TI 83 BinomPDF y TI 83 BinomCDF pueden ayudarlo a resolver preguntas de probabilidad binomial en segundos. Las probabilidades binomiales implican dos resultados: éxito o fracaso. Por ejemplo, si estuviera lanzando una moneda para ver cuántas caras obtendría, si la moneda cae en cara, sería un «éxito». La diferencia entre las dos funciones es que una (BinomPDF) es para un solo número (por ejemplo, tres lanzamientos de una moneda), mientras que la otra (BinomCDF) es una probabilidad acumulada (por ejemplo, 0 a 3 lanzamientos de una moneda) .

Para probabilidades de un solo número (como dos, tres, una docena o algo similar, querrá usar BinomPDF .

Calculadora BinomCDF TI 83: Pasos

Mira el video de los pasos:

Ejemplo de función binomCDF TI83 Mira este video en YouTube .
¿No puedes ver el vídeo? Haga clic aquí

Problema de ejemplo: el promedio de bateo de Bob es .321. Si se acerca al plato cuatro veces, encuentre la probabilidad de que consiga hasta tres hits.

Paso 1: presione 2nd VARS para obtener la opción «DISTR». Desplácese hacia abajo hasta “A:BinomCDF” y luego presione ENTER.

Paso 2: Introduzca el número de intentos. Bob batea cuatro veces, por lo que el número de intentos es 4 . Presione 4 seguido de una coma.

Paso 3: Ingrese la probabilidad de éxito, P . Bob tiene un promedio de bateo de .321 , así que ingrese .321 seguido de una coma.

Paso 4: Ingrese el valor X. Queremos saber cuál es la probabilidad de que Bob obtenga hasta tres aciertos, así que ingrese 3, seguido de un paréntesis de cierre.

Paso 5: Presione ENTER para el resultado. Las posibilidades de Bob de obtener hasta tres hits son .989 .

Sugerencia : en lugar de desplazarse hacia abajo hasta «A: BinomCDF», puede presionar ALFA y luego MATEMÁTICAS.

¡Así es como se usa la calculadora BinomCDF TI 83!

Probabilidad Binomial TI 83: BinomPDF.

Esta sección le dice cómo usar la función BinomPDF para calcular una cantidad exacta (como tres veces, o dos, o una docena de ocurrencias). Para probabilidades acumulativas (como «hasta cierto número» o «entre 5 y 10» o «menos de 6» o algo similar, querrá usar BinomCDF .

Ejemplo de problema : Sue tiene un promedio de bateo de .270. Si ella está al bate tres veces, ¿cuál es la probabilidad de que consiga exactamente dos hits?

Paso 1: presione 2nd VARS para obtener la opción «DISTR». Presione 0 para «binomPDF».

Paso 2: Ingrese el número de intentos de la pregunta. Sue batea tres veces, por lo que el número de intentos es 3 . Presione 3 y presione la tecla ,.

Paso 3: Ingrese la probabilidad de éxito, P . El promedio de bateo de Sue es .270 , así que ingrese .270, luego presione la tecla , .

Paso 4: Ingrese el valor X. Queremos saber las posibilidades de Sue de obtener exactamente dos aciertos, así que ingrese 2 y luego presione ).

Paso 5: Presiona Enter para el resultado. Las posibilidades de Sue de acertar exactamente dos hits son .159651 .

Advertencia : BinomialPdf es una probabilidad exacta para un valor de x. Si desea encontrar una probabilidad acumulativa (por ejemplo, ¿cuáles son las posibilidades de John de obtener 0 o 1 aciertos?), necesitará usar la función BinomCDF .

¡Así es como encontrar una probabilidad binomial en la TI 83!

¿Perdiste tu guía? Descargue uno nuevo aquí en el sitio web de TI.

¡ Visite nuestro canal de Youtube para obtener más ayuda y consejos sobre estadísticas!

Referencias

Agresti A. (1990) Análisis de datos categóricos. John Wiley and Sons, Nueva York.
Everitt, BS; Skrondal, A. (2010), The Cambridge Dictionary of Statistics , Cambridge University Press.
Gonick, L. (1993). La guía de dibujos animados de estadísticas . Harper Perennial.
Vogt, WP (2005). Diccionario de estadística y metodología: una guía no técnica para las ciencias sociales . SABIO.