Contenido de este artículo
- 0
- 0
- 0
- 0
Actualizado el 26 de febrero de 2022, por Luis Benites.
¿Qué es la Distribución de Von Mises?
La distribución de Von Mises (también llamada normal circular o distribución de Tikhonov) es una distribución de probabilidad continua con un rango de 0 a 2π. Es similar a la distribución normal , excepto que las coordenadas se colocan en un plano circular. La distribución de von Mises se puede considerar como un caso especial de la distribución de Von Mises-Fisher , que es una extensión de la distribución a esferas multidimensionales.
La distribución fue descrita por primera vez por Richard von Mises en 1918 como una forma de modelar la distribución de pesos atómicos. Ahora se usa para modelar una variedad de fenómenos que incluyen:
- Movimiento browniano (Física),
- Epidemiología (propagación de enfermedades),
- Alineación de interferencias (procesamiento de señales),
- Algoritmos de preservación de la privacidad en (Machine Learning).
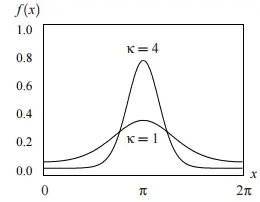
PDF para valores de μ = π y κ de 1 y 4.
La forma general del PDF de Von Mises es: Donde:
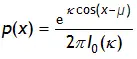
- μ es la dirección media de la distribución. μ puede ser cualquier número real.
- κ es un parámetro de forma llamado «concentración», que es recíproco a la dispersión; 1/κ es comparable a la varianza : las concentraciones altas implican una varianza baja y viceversa. Los valores de κ deben ser números reales no negativos . Si κ = 0, la distribución es uniforme ; si los valores de κ son grandes, la distribución se convierte en una distribución normal.
- I 0 0(κ) es la función de Bessel modificada con orden cero. Se define para todo κ como:
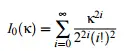
Las abreviaturas X ~ von Mises (κ, μ) o X ~ CN (κ, μ) se utilizan para indicar que la variable aleatoria X tiene una distribución de von Mises con parámetro de forma κ y parámetro de ubicación μ.
FCD
La función de distribución acumulada para esta distribución es:
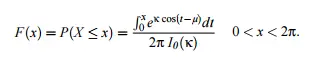
Otras características
La mediana y la media de X es cero.
Los siguientes son matemáticamente intratables (difíciles o casi imposibles de resolver):
- función característica ,
- función de riesgo ,
- función de distribución inversa,
- Curtosis ,
- Varianza de la población ,
- sesgo _
Software
La distribución de Von Mises no forma parte de los paquetes estadísticos más populares. Sin embargo, tiene opciones como complementos o un paquete especializado de estadísticas direccionales.
- Dataplot (código abierto) tiene un comando VONPPF incorporado .
- Oriana para Windows “…calcula las formas especiales de las estadísticas de muestras e intermuestras requeridas para los datos circulares (p. ej., ángulos o direcciones medidos en grados, hora del día, día de la semana, mes del año, etc.)”. El precio minorista actual es de alrededor de $ 400.
- Circstats es un paquete complementario para R (código abierto).
- Circstat es un complemento gratuito para MatLab.
Referencias
Grafarend, E. y Awange. J. (2012) Aplicaciones de Modelos Lineales y No Lineales: Efectos Fijos, Efectos Aleatorios. Springer Science & Business Media, 15 de agosto.
Kotz, S.; et al., editores. (2006), Enciclopedia de Ciencias Estadísticas , Wiley.
Von Mises, R. (1981): Uber die Ganzzahligkeit der Atomgewichte und verwandte Gragen. física Z. 19 (1918), 490-500.
Redactor del artículo
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo:
