Actualizado por ultima vez el 26 de febrero de 2022, por Luis Benites.
Un estimador bayesiano es un estimador de un parámetro desconocido θ que minimiza la pérdida esperada para todas las observaciones x de X.
En otras palabras, es un término que estima su parámetro desconocido de una manera que pierde la menor cantidad de precisión (en comparación con haber utilizado el valor real de ese parámetro).
Estimadores de Bayes y la función de pérdida
Un estimador bayesiano es una función de variables aleatorias observables , variables que observaste en el proceso de tu investigación. Llame a sus variables observables X 1 X 2 …X n
Sus datos pueden ser representados por la función f(x|θ), donde θ es una distribución previa . Sin embargo, no conoce el valor real de θ, por lo que debe estimarlo. Un estimador de θ es una función de valor real δ(X 1 … X n ), que no debe confundirse con Δx en cálculo , lo que significa un pequeño cambio.
La función de pérdida L(θ, a ) donde a ε R, es también una función de valor real de θ. Nuestra estimación aquí es a , y L(θ, a ) nos dice cuánto perdemos al usar a como estimación cuando el verdadero valor real de un parámetro es θ.
Hay diferentes funciones de pérdida posibles . Por ejemplo, la función de pérdida de error al cuadrado viene dada por L(θ a ) = (θ – a ) 2 . La función de pérdida de error absoluta sería L(θ a ) = |θ – a |.
En la primera definición de estimador bayesiano al comienzo de esta página, dijimos que era un estimador que minimizaba la pérdida esperada. Esa pérdida está representada por una función de pérdida como una de las que acabamos de describir.
Podemos encontrar la pérdida mínima esperada integrando . Para un X = x dado, la pérdida esperada (E) es: En esta fórmula, Ω es el rango sobre el cual se define θ. p(θ | x) es la función de verosimilitud ; la distribución previa del parámetro θ sobre las observaciones x . Llame a * (x) el punto donde alcanzamos la pérdida mínima esperada. Entonces, para a*(x) = δ*(x), δ*(x) es la estimación bayesiana de θ.
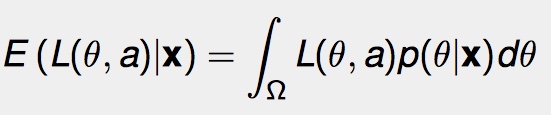
Estimador Bayesiano: Referencias
Brynjarsdottir, Jenny. STAT 611 Apuntes de clase: Clase 12, Estimación.
Recuperado de https://www2.stat.duke.edu/courses/Fall12/sta611/Lecture12.pdf el 9 de marzo de 2018
Shiryaev, AN Estimador bayesiano, Enciclopedia de Matemáticas. Recuperado de: http://www.encyclopediaofmath.org/index.php?title=Bayesian_estimator&oldid=19043 el 4 de marzo de 2018.
Zhu, Wei. Inferencia Bayesiana para la Decisión Normal. Recuperado de http://www.ams.sunysb.edu/~zhu/ams571/Bayesian_Normal_wide.pdf el 4 de marzo de 2018

