Actualizado por ultima vez el 11 de diciembre de 2021, por Luis Benites.
La distribución normal gamma (también llamada distribución normal gaussiana , distribución GN o distribución gamma normal ) es una distribución de probabilidad compuesta bivariada para la suma de una variable aleatoria gamma y una variable aleatoria normal/gaussiana. Es el previo conjugado (de la estadística bayesiana ) de una distribución normal con media y precisión desconocidas [1]. «Conjugado» aquí significa que la superficie es una gamma normal tanto antes como después de que se hayan tenido en cuenta los resultados históricos. A medida que recopila más datos de muestra, los parámetros cambia y por lo tanto la forma de la superficie cambia también.
La distribución tiene cuatro parámetros: mu (μ), kappa (κ, alfa α y beta β. La distribución puede describir una multitud de formas de superficie, dependiendo de estos cuatro valores (también conocidos como parámetros).
Si las variables aleatorias X, Y tienen una distribución gamma normal, entonces la distribución marginal de Y es una distribución gamma con parámetros α, β. La distribución condicional de X, dado Y, es una distribución normal con valor esperado μ y desviación estándar registrada κ -log(Y)/2.
Función de Densidad de Probabilidad para la Distribución Gamma-Normal
Si X ~ N(μ, σ 2 ) y σ ~ gamma inversa (α, β), entonces la PDF de la variable aleatoria X viene dada por [2]: Para -∞ x ∞.
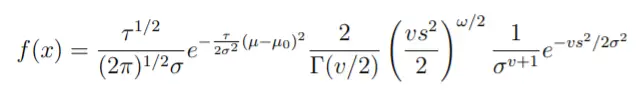
Referencias
[1] Bernardo, JM; Smith, AFM (1993) Teoría bayesiana, Wiley. ISBN 0-471-49464-X[2] Teorema. Recuperado el 7 de diciembre de 2021 de: http://www.math.wm.edu/~leemis/chart/UDR/PDFs/NormalGammanormal.pdf

