Actualizado por ultima vez el 26 de abril de 2022, por Luis Benites.
¿Qué es una función de riesgo?
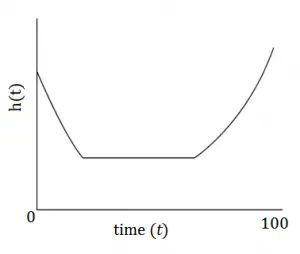
La función de riesgo h(t) que muestra las posibilidades de muerte de un ser humano a cualquier edad en particular.
La función de riesgo (también llamada fuerza de mortalidad , tasa de falla instantánea, tasa de muerte instantánea o tasa de falla específica por edad ) es una forma de modelar la distribución de datos en el análisis de supervivencia. El uso más común de la función es modelar la probabilidad de muerte de un participante en función de su edad . Sin embargo, se puede utilizar para modelar cualquier otro evento de interés dependiente del tiempo.
Más específicamente, la función de riesgo modela qué períodos tienen las posibilidades más altas o más bajas de un evento . La función se define como el riesgo instantáneo de que suceda el evento de interés, dentro de un marco de tiempo muy estrecho. (Nota: si está familiarizado con el cálculo , puede reconocer que esta medida instantánea es la derivada en un punto determinado).
Las funciones de riesgo y las funciones de supervivencia son alternativas a las funciones tradicionales de densidad de probabilidad (PDF ). Son más adecuados que los archivos PDF para modelar los tipos de datos que se encuentran en el análisis de supervivencia.
Condicional y variaciones
La función de riesgo es una tasa de falla condicional, en el sentido de que es condicional que una persona haya sobrevivido hasta el tiempo t . En otras palabras, la función en el año 10 solo se aplica a aquellos que estaban realmente vivos en el año 10; no cuenta los que murieron en períodos anteriores.
Hay otras variaciones de la función, además de la tasa condicional. El método Kaplan Meier (KM) usa tasas, no tiene límite superior y es el preferido para ensayos clínicos (Fink & Brown, 2006). Por el contrario, con el método actuarial , la función de riesgo es una proporción, con valores entre 0 y 1.
Fórmula
La fórmula de la función de riesgo es: Donde:
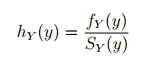
- f Y (y) = la función de densidad de probabilidad del tiempo de supervivencia Y,
- S Y = la función Superviviente (la probabilidad de sobrevivir más allá de un cierto punto en el tiempo)
Referencias
Der, G. y Everitt, B. (2007). Estadísticas básicas usando SAS Enterprise Guide: Una introducción. Instituto SAS.
Fink, S., Brown, R. (2006). Análisis de supervivencia. Gastroenterol Hepatol (Nueva York). Puede; 2(5): 380–383. Recuperado el 28 de mayo de 2018 de aquí (https://www.ncbi.nlm.nih.gov/pmc/articles/PMC5338193/).
