Ley de Benford (la ley del primer dígito): definición simple, ejemplos

Actualizado el 17 de mayo de 2022, por Luis Benites.

¿Qué es la Ley de Benford?

La ley de Benford (también llamada ley del primer dígito ) establece que los primeros dígitos en una colección de conjuntos de datos probablemente serán pequeños . Por ejemplo, la mayoría de los números de un conjunto (alrededor del 30 %) tendrán un dígito inicial de 1, cuando la probabilidad esperada es del 11,1 % (es decir, uno de nueve dígitos). A esto le sigue alrededor del 17,5% que comienza con un número 2. Este es un fenómeno inesperado; Si todos los números principales (del 0 al 9) tuvieran la misma probabilidad, cada uno ocurriría el 11,1 % de las veces. En pocas palabras, la ley de Benford es una distribución de probabilidad para la probabilidad del primer dígito en un conjunto de números (Frunza, 2015).

La ley solo funciona para el significado ^* S(x) (Hill y Berger, 2017), que es esencialmente cualquier número colocado en un formato estándar. Para encontrar el significado:

• Encuentre el primer dígito distinto de cero,
• Mueva el punto decimal inmediatamente a la derecha de ese dígito,
• Ignora la señal.

Por ejemplo, 2092 y −0,02092 tienen S(x) = 2,092.

*El significado es parte de un número en aritmética de punto flotante y notación científica; Cualquier número positivo x puede escribirse como S(x) · 10 ^k . Por ejemplo, el número 8201,24709 se puede escribir como 8,20124709 * 10 ³ en notación científica. El significado es 8.20124709 (el 3 se llama exponente y el 8 es el dígito inicial).

Fórmula

La fórmula para la ley de Benford es: Donde “d” (el primer dígito) es un número del 1 al 9. Por ejemplo, la probabilidad de que el primer dígito sea 1 es: La siguiente imagen muestra la distribución de probabilidad para todos los dígitos:

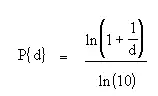
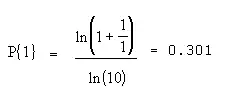
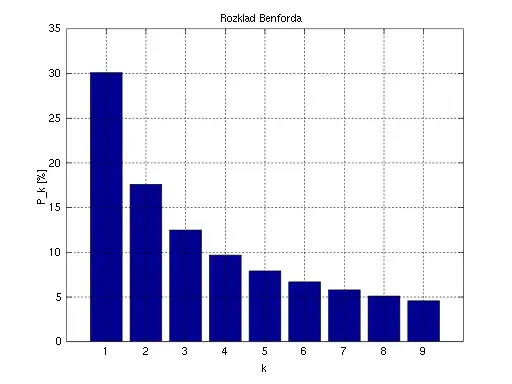
La distribución de los primeros dígitos, según la ley de Benford.

La ley de Benford también se puede usar para hacer predicciones sobre cuáles serán los dígitos principales segundo, tercero y posteriores, así como las probabilidades de ciertas combinaciones de números.

La ley de Benford no se aplica a todos los conjuntos de números, pero generalmente se aplica a grandes conjuntos de números naturales con alguna conexión como:

• valores bursátiles de las empresas,
• Datos encontrados en textos, como Reader’s Digest o una copia de Newsweek.
• Datos demográficos, incluidas las poblaciones estatales y municipales,
• datos del impuesto sobre la renta,
• Tablas matemáticas, como logaritmos,
• tasas de drenaje del río,
• Datos científicos.

Por lo general, la ley no se aplica a los conjuntos de datos que tienen un mínimo y un máximo establecidos , como las tasas de interés o los salarios por hora. Si se asignan números, en lugar de que ocurran naturalmente, tampoco seguirán la ley. Ejemplos de números asignados incluyen: códigos postales, números de teléfono y números de Seguro Social.

Usos

Un uso práctico de la ley de Benford es la detección de fraudes y errores. Se espera que un gran conjunto de números siga la ley, por lo que los contadores, auditores, economistas y profesionales de impuestos tienen un punto de referencia sobre cuáles son los niveles normales de cualquier número en particular en un conjunto.

• En la segunda mitad de la década de 1990, el contador Mark Nigrini descubrió que la ley de Benford puede ser una prueba de bandera roja efectiva para las declaraciones de impuestos fabricadas ; Los datos fiscales verdaderos generalmente siguen la ley de Benford, mientras que las declaraciones inventadas no lo hacen.
• La ley se usó en 2001 para estudiar los datos económicos de Grecia, con la implicación de que el país pudo haber manipulado los números para unirse a la Unión Europea.
• Los esquemas Ponzi se pueden detectar usando la ley. Los rendimientos poco realistas, como los pretendidos por la estafa de Maddoff, están muy lejos de la distribución de probabilidad de Benford esperada (Frunza, 2015).

Historia

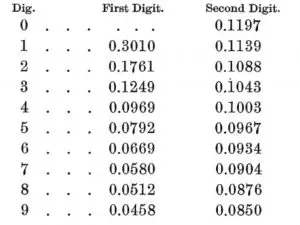
Aunque se llama ley de Benford, él no fue la primera persona en estudiar el fenómeno. El astrónomo Simon Newcomb (1881), futuro presidente de la Sociedad Matemática Estadounidense , sentó las bases de la ley después de mirar tablas de logaritmos. Se dio cuenta de que las primeras páginas estaban más gastadas y manchadas que las páginas posteriores. Newcomb concluyó que «el primer dígito es más a menudo 1 que cualquier otro dígito» y publicó sus hallazgos en Note on the Frequency of Use of the Different Digits in Natural Numbers , que apareció en The American Journal of Mathematics. Newcomb incluyó una tabla para las probabilidades del primer y segundo dígito, d : el célebre matemático francés Henri Poincaré desarrolló la idea aún más, en
Répartition des décimales dans une table numérique (distribución de decimales en tablas numéricas). La ley recibe su nombre del físico de la compañía General Electric, Frank Benford , quien redescubrió los hallazgos de Newcomb y los popularizó. Benford usó varios conjuntos de números para demostrar la ley. Estudió 20,229 observaciones de 20 conjuntos de datos diferentes, que incluyen:

• Una lista de direcciones de calles,
• Pesos moleculares y calores específicos de miles de productos químicos,
• Superficies de 335 ríos,
• secuencias matemáticas,
• Un número de Reader’s Digest.

Benford publicó sus hallazgos en el artículo La ley de los números anómalos en las Actas de la Sociedad Filosófica Estadounidense (1938). Como ejemplo, encontró los siguientes porcentajes en Reader’s Digest (recuento total, 308 instancias):

• 1 = 33,4%
• 2 = 18,5%
• 3 = 12,4%
• 4 = 7,5%
• 5 = 7,1%
• 6 = 6,5%
• 7 = 5,5%
• 8 = 4,9%
• 9 = 4,2%

Benford mismo señaló que un conjunto de datos individuales, como este, puede no ajustarse a la ley. Sin embargo, la media de un gran número de conjuntos de datos sí lo hará.

«Prueba» que funciona

La ley es difícil de probar matemáticamente, ya que es más parecida a una teoría que funciona (algo así como la regla de la multiplicación ). Se han hecho muchos intentos para explicar el fenómeno, desde los pensamientos iniciales de Benford sobre la naturaleza logarítmica de los datos hasta el marco de probabilidad de Hill, que utilizó mezclas de diferentes distribuciones de probabilidad para explicarlo parcialmente. En el momento de escribir este artículo, aún no ha habido una respuesta completa a la pregunta de por qué funciona. Pero funciona, más o menos. Diaconis y Freedman (1979) sugieren que Benford fue bastante liberal con la forma en que redondeó los números para que los datos se ajustaran mejor a la ecuación.

mi propio experimento

Quizás la mejor manera de convencerse de que la ley funciona es elegir un libro o una revista al azar y hacer una lista/ordenar los números: alrededor del 30 % de los números recopilados de cualquier edición comenzarán con el número 1. Lo hice yo mismo, por Edición del 16 de octubre de 2017 de Time . Este resultó ser el material de lectura más cercano a donde estaba sentado, lo que probablemente podría calificar como aleatorio ya que hay muchos libros y revistas en mi casa.

El resultado: de 702 números totales, 201 (29%) comenzaron con el número 1.

Nota técnica: solo conté el primer número de una cadena. Por ejemplo, 5 03(c)(3) o 2 017-22.

Algunas cosas que noté sobre la naturaleza de los números.

Esto puede explicar parcialmente por qué hay más «1» que cualquier otro número:

• Las estadísticas a menudo se citan como «1 en 8», o «1 de 9», o algún otro «1 de nnn». Es raro que vea otro número como «3 de 10» o «4 de 17».
• Cualquier lista definitivamente tendrá 11 unos en los primeros 20 números (1…10, 11, 12, 13, 14, 15, 16, 17, 18, 19).
• La mayoría de los libros tienen números de página y la mayoría de los libros o revistas tienen al menos 20 páginas (lo que significa 11 unidades). Las revistas y los libros más cortos tendrán menos 9, 8 y 7, pero siempre tendrán esos 11 números que comienzan con 1.
• La misma lógica se aplica a las edades de las personas. Hay muchas más personas vivas entre los 11 y los 19 años que las que tienen entre 80 y 90 años.
  Alrededor de un tercio de los días del mes comienzan con un 1 (1, 10, 11, etc.). Ningún día del mes comienza con 4, 5, 6, 7, 8 o 9.
• Como se trata de la revista Time, hay muchas fechas. Y como estamos en 2017, hay muchas menciones de 2017 (de hecho, muchas 2xxx). Plantea la pregunta: ¿los problemas del siglo pasado (19xx) influirían en los números de otra manera? Probablemente. Esta es la razón por la cual una prueba de una muestra no sirve para mucho. ¡Pero no tengo el tiempo o la inclinación para hacer de esta una prueba de muestra grande!
• Los números de teléfono gratuitos comienzan con 1 (por ejemplo, 1-866-821-7406). En una revista de noticias, o cualquier revista con anuncios, hay muchos números gratuitos.

En conclusión, debería parecer obvio que habrá más “1” que cualquier otro número, porque aquí es donde empezamos a contar cualquier cosa .

Referencias

Benford, F. «La ley de los números anómalos», Actas de la Sociedad Filosófica Estadounidense, 78, 551–572. 1938.
Diaconis, P. y Freedman, D. “Sobre los porcentajes de redondeo”, J. Amer. Estadística Asoc., 74 (1979) 359–364. MR 81d:62014
Frunza, M. (2015). Resolución de la delincuencia moderna en los mercados financieros: análisis y estudios de casos. Prensa Académica.
Hill, TP «El fenómeno del primer dígito». Amer. ciencia 86, 358-363, 1998.
Newcomb, S. “Nota sobre la frecuencia del uso de dígitos en números naturales”. Amer. J. Matemáticas. 4, 39-40, 1881.
Nigrini, N. (1999). Tengo tu número. Recuperado el 8 de noviembre de 2017 de: https://www.journalofaccountancy.com/issues/1999/may/nigrini.html
Poincaré, H. Répartition des décimales dans une table numérique. pp 313-320 en: Calcul des Probabilités, Gauthier-Villars, París.
Rauch, B. et. Alabama. «Realidad y ficción en los datos económicos gubernamentales de la UE». Revista Económica Alemana .