Modelo anidado, ANOVA y factores: definiciones simples y ejemplos

Actualizado el 17 de mayo de 2022, por Luis Benites.

¿Qué es un modelo anidado?

Muy simple, «anidado» significa que un modelo es un subconjunto de otro. Por ejemplo, tome un modelo para los resultados del embarazo que incluya cuatro variables independientes categóricas :

• Edad,
• Peso,
• Condiciones preexistentes,
• Factores hereditarios.

Se pueden derivar varios modelos más pequeños a partir de este principal, y cada uno está «anidado» dentro del modelo principal. Por ejemplo:

1. Edad y peso,
2. Peso y condiciones preexistentes,
3. Edad y factores hereditarios.

Básicamente, si puede obtener un modelo restringiendo los parámetros de otro, esos modelos están anidados. Por ejemplo, el conjunto de modelos de distribución normal contiene un número infinito de modelos anidados, incluidas las distribuciones normales con medias de 0, 1 o 99.

Usos

Los modelos anidados se utilizan para varias pruebas y análisis estadísticos, incluida la regresión múltiple , las pruebas de razón de verosimilitud , el análisis conjunto y las alternativas independientes de las irrelevantes (IIA). Si bien la definición anterior debería darle una idea general de lo que es un modelo anidado, la definición se vuelve un poco más técnica dependiendo de dónde esté usando. Por ejemplo:

En la regresión múltiple y el modelado de ecuaciones estructurales (SEM) , la idea es la misma: que un modelo está anidado dentro de otro. Más técnicamente, ambos modelos deben tener términos idénticos y uno de los modelos debe tener uno o más términos adicionales. Por ejemplo:

• y = β ₀ + β ₁ x ₁ + β ₂ x ₂ + 10
• y = β ₀ + β ₁ x ₁ + β ₂ x ₂ + β ₃ x ₁ x ₂ + 10

El modelo más grande se llama modelo completo y el modelo más pequeño se llama modelo reducido.

Precaución : no todos los modelos anidados son tan obvios como los que he resaltado anteriormente. Rigdon (1999) sugiere precaución al decidir analizar modelos anidados debido a este hecho. En el momento de escribir este artículo, no existe ningún software que pueda analizar si dos modelos estructurales diferentes son similares (Bentler y Satorra).

Factores anidados

Los factores anidados ‘encajan unos dentro de otros’.

Como recordatorio, un «factor» es un conjunto de variables observadas que tienen patrones de respuesta similares. Dos factores A y B están anidados si hay un conjunto completamente diferente de valores de B para cada valor de A.

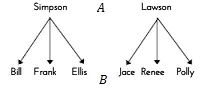Como ejemplo, digamos que el factor “A” es la familia y el factor “B” son los niños . Un niño puede ser Simpson o Lawson, pero no ambos. Bill, Frank o Ellis son Simpson; Jace, Renee o Polly son Lawson. Estos dos factores (familia/niño) están anidados porque cualquier niño existe en una sola familia. En términos más formales, decimos que todo valor de B existe para uno y sólo un valor de A.

Ejemplos de factores anidados.

Imagine que un probador de productos necesita probar los niveles de plomo y arsénico en frijoles horneados enlatados producidos por cierta marca conocida. Podría visitar tres fábricas diferentes, probar dos lotes diferentes en cada fábrica y abrir cinco latas por lote. Factory, Batch # y Can ID # son tres variables diferentes, pero están anidadas. Cada lata existe solo en un lote en particular, y cada lote existe en una sola fábrica.

O supongamos que se encuestó a una clase de niños sobre su refrigerio favorito, ya sea dulce o salado (factor A). Algunos dijeron que preferían los bocadillos salados, otros dijeron que les gustaban más los bocadillos dulces. Entre los niños a los que les gustaban los snacks salados se encontraban marcas específicas (factor B). Algunos niños preferían Cheez-its(1), nachos(2), palomitas picantes(3) o Slim Jims(4). Otros niños preferían las meriendas dulces: helado(1), chocolate(2), fruta(3) y golosinas(4).

Los dos factores A y B están anidados. Cada una de las variables de refrigerio se incluye exactamente en una de las distinciones de variables dulce/salado.

Notación para factores anidados

El subíndice j(i) indica que el factor indexado por j está anidado en el factor indexado por i. En el ejemplo de refrigerio anterior, podría indexar A con i = 1, 2 y B con j = 1, 2, 3, 4. Tenga en cuenta que aunque la indexación de B (marca) se repite en las dos instancias de A (dulce o salado), los valores reales de B son diferentes para ambos. Por ejemplo, 1(2) (preferencia por los nachos) no es lo mismo que 2(2) (preferencia por el chocolate).

Determinar si los factores están anidados

A veces, no es inmediatamente obvio si los factores están anidados o no. La forma más fácil de verificar es hacer una tabla; si todos los valores de B son distintos de cero para un solo valor de A, B está anidado en A.

En la tabla anterior, los números se asignaron aleatoriamente a cada valor de cada variable. Se eliminaron las columnas sin datos (cero en todas partes); Por ejemplo, todas las instancias de B = 5 están en A = 2. La columna A = 1, B = 5 está vacía, por lo que no se incluye en la tabla.

¿Qué es ANOVA anidado?

Un ANOVA anidado (también llamado ANOVA jerárquico ) es una extensión de un ANOVA simple para experimentos en los que cada grupo se divide en dos o más subgrupos aleatorios. Comprueba si hay variación entre grupos o dentro de subgrupos anidados de la variable de atributo. Debe usar ANOVA anidado cuando tenga:

• Una variable de medida ,
• Dos o más variables nominales anidadas (factores).

Ejemplos

Supongamos que desea investigar la brecha salarial entre hombres y mujeres. También piensa que la altura afecta los salarios (lo cual es cierto; consulte la historia de The Atlantic sobre Por qué las personas altas ganan más ) al igual que la obesidad (también es cierto: consulte la historia de Forbes El precio de la obesidad ). Sus factores o niveles (sexo, altura, peso) están anidados unos dentro de otros. Por ejemplo, el «peso» no es un factor independiente, está anidado bajo masculino/femenino. La siguiente imagen muestra el modelo jerárquico :

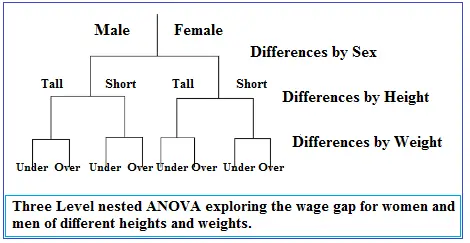
En el siguiente ejemplo, se tomaron muestras de 5 plántulas diferentes de 5 flores diferentes en dos campos diferentes A y B:

Modelo I y Modelo II en ANOVA anidado

Un modelo I ANOVA (también llamado modelo de efectos fijos) es donde el experimentador fija los tratamientos. Por ejemplo, si está comparando cómo los diferentes pesos afectan la salud, puede elegir rangos de peso específicos. Si un ANOVA anidado tiene el nivel más alto del Modelo I, se denomina ANOVA anidado de modelo mixto.

Los ANOVA del modelo II son aquellos en los que los tratamientos son aleatorios y no fijos. Por ejemplo, en lugar de que el investigador elija los pesos, estos se elegirían al azar. Si un ANOVA anidado tiene un nivel más alto de modelo II, se denomina ANOVA anidado de modelo II puro.

Diseños anidados y cruzados

Si bien los modelos anidados se pueden representar mediante un gráfico puramente jerárquico, como los de arriba, los modelos cruzados implican algún cruce entre los niveles de la variable independiente . Un ejemplo de un modelo cruzado puro es donde el maestro A y el maestro B enseñan a dos grupos de estudiantes diferentes formas de resolver problemas matemáticos. Como todos los estudiantes de ambos grupos están expuestos a los métodos del maestro A y del maestro B, el modelo es cruzado. Si estuviera anidado, un grupo de estudiantes solo experimentaría los métodos de un maestro.

Los diseños cruzados son preferibles porque detectan mejor las diferencias entre grupos que los modelos anidados. Sin embargo, puede que no sea posible usar siempre modelos cruzados; algunos experimentos requieren el uso de modelos anidados.

En muchos experimentos, es posible que no quede claro si su modelo está anidado o cruzado y, en algunos casos, es posible que tenga una combinación de ambos. Averiguar si su diseño está anidado o no puede ser un desafío. Dibujar un gráfico jerárquico como los de arriba puede ayudar.

El ejemplo anterior de la brecha salarial entre hombres y mujeres se cruzaría en lugar de anidarse si fuera posible que los niveles de los factores se cruzaran. Por ejemplo, si un hombre pudiera ser bajo y alto, o de peso normal y sobrepeso. Si bien esto es teóricamente posible (por ejemplo, podrías tener gemelos, uno de los cuales tiene sobrepeso y el otro peso normal), en este caso el escenario no se cruza.

Referencias

Bentler, P. y Satorra, A. (2010). Pruebas de anidamiento y equivalencia de modelos . Métodos Psicológicos. 2010 junio; 15(2): 111–123. Recuperado el 19/9/2016 de http://www.ncbi.nlm.nih.gov/pmc/articles/PMC2929578/.
Carriquiry, A. Regresión múltiple. Recuperado el 19/9/2016 de: http://www.public.iastate.edu/~alicia/stat328/Multiple%20regression%20-%20nested%20models.pdf
Doncaster & Davey (2007). Análisis de varianza y covarianza: cómo elegir y construir modelos para las ciencias de la vida. Prensa de la Universidad de Cambridge.
Estadísticas de Purdue. Una mirada a los factores anidados. Recuperado el 17 de septiembre de 2017 de: http://www.stat.purdue.edu/~bacraig/notes1/topic19.pdf
Rigdon, EE (1999). Uso del método de rangos de Friedman para la comparación de modelos en el modelado de ecuaciones estructurales. Modelado de ecuaciones estructurales, 6(3), 219-232