Actualizado por ultima vez el 24 de diciembre de 2021, por Luis Benites.
La corrección de Huynh-Feldt es una corrección para las violaciones de la esfericidad .
Si la prueba de la prueba de esfericidad de Mauchly arroja un valor p pequeño , debe aplicar una corrección al índice de no esfericidad (llamado índice de caja, ε):
- Cuando ε ≤ 0,75 (o no sabe cuál es el valor de la estadística), utilice la corrección de Greenhouse-Geisser. Esta es una corrección conservadora que aumenta el riesgo de error de tipo II .
- Cuando ε > 0,75, utilice la corrección de Huynh-Feldt. Abdi (2010) describe esta corrección como más eficiente y más poderosa que la corrección Greenhouse-Geisser.
Existe cierto debate sobre qué corrección es la «mejor». Abdi (2010) afirma que, de los dos, se prefiere el Huynh-Feldt porque el Greenhouse-Geisser es demasiado conservador. Sin embargo, algunos consideran que la corrección HF es demasiado liberal y sobrestima la esfericidad (p. ej., Maxwell y Delaney, 1990).
Fórmula de corrección de Huynh-Feldt
La fórmula para la corrección de Huynh-Feldt (de Abdi, 2010) es: Donde:
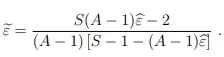
- S = Número de sujetos,
- A = Número de tratamientos,
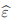= Estimación para ε.
Referencias
Abdi, H. La corrección Greenhouse-Geisser. En Neil Salkind (Ed.), Encyclopedia of Research Design.
Thousand Oaks, CA: Sabio. 2010. Recuperado el 1 de julio de 2019 de: https://www.utdallas.edu/~herve/abdi-GreenhouseGeisser2010-pretty.pdf
Everitt, BS; Skrondal, A. (2010), The Cambridge Dictionary of Statistics , Cambridge University Press.
Invernadero, SW y Geisser, S. (1959). Sobre métodos en el análisis de datos de perfil. Psychometika, 24, 95–112
Huynh, H., & Feldt, LS (1976) Estimación de la corrección Box para grados de libertad a partir de
datos muestrales en diseños de bloques aleatorizados y parcelas divididas. Revista de estadísticas educativas,
1, 69–82
Kotz, S.; et al., editores. (2006), Enciclopedia de Ciencias Estadísticas , Wiley.
Maxwell, SE y Delaney, HD (1990). Diseño de experimentos y análisis de datos: una perspectiva de comparación de modelos. Belmont: Wadsworth.
