Actualizado por ultima vez el 23 de diciembre de 2021, por Luis Benites.
¿Qué es la distribución robusta de solitones?
El análisis de los códigos LT (Luby transform) se basa en el análisis del algoritmo de decodificación, los procesos LT. Cada símbolo de código LT se genera seleccionando aleatoriamente el grado del símbolo de código, d , entre 1 y k . La distribución Robust Soliton es una distribución de grados , una forma de construir un buen grado de codificación de símbolos [1]. El distribuido se construye de modo que el decodificador pueda recuperar datos de un poco más de k símbolos de código con probabilidad > 1 – δ, donde δ está entre 0 y 1 [2].
La distribución se utiliza en la teoría de la codificación, específicamente en la teoría de los códigos correctores de borrado. Utiliza la redundancia de información para compensar los errores de transmisión que se presentan como datos faltantes.
Fórmulas de distribución de solitones ideal y robusta
Liby [2] introdujo dos distribuciones, la distribución de solitones ideal y la distribución de solitones robusta .
La distribución de solitones ideal , se define como una distribución de probabilidad con un solo parámetro K : optimiza la probabilidad esperada de que haya un bloque fuente decodificable en cada iteración del proceso. Sin embargo, existe una probabilidad inaceptable de fallar en alguna iteración. Este problema se puede abordar con la distribución robusta de solitones, que agrega un conjunto adicional de valores [3]:
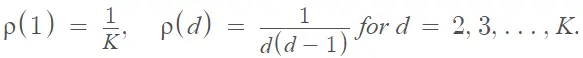
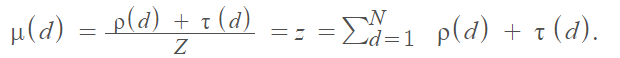
La distribución de solitones ideal tiene un pico en 2, mientras que el componente extra en la distribución robusta agrega un pico adicional en el valor K / R .
Referencias
[1] Proyecto 5: Proyecto Capstone: Códigos LT. Recuperado el 14 de julio de 2021 de: http://cs.brown.edu/courses/csci1680/f17/content/lt.pdf[2] Luby, M. (2002). Códigos LT, Proc. del 43º Simposio Anual IEEE. sobre Fundamentos de Comp. Sc., págs. 271-280, Vancouver, Canadá, noviembre.
[3] Joshi et al. Códigos de fuentes . Recuperado el 14 de julio de 2021 de: https://www.andrew.cmu.edu/user/gaurij/FountainCodes.pdf

